Для решения запишем формулу бинома Ньютона:
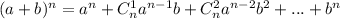
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение 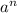 .
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение 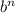 .
.
Рассмотрим многочлен 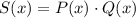 , где:
, где:
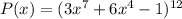
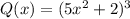
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена 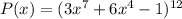 :
:
- степень определяется выражением 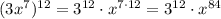 , то есть степень равна 84
, то есть степень равна 84
- свободный член равен 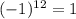
Для многочлена 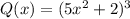 :
:
- степень определяется выражением 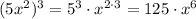 , то есть степень равна 6
, то есть степень равна 6
- свободный член равен 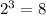
Наконец, для многочлена 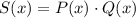 получим:
получим:
- степень определяется выражением 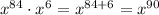 , то есть степень равна 90
, то есть степень равна 90
- свободный член равен 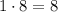
Сумма степени и свободного члена многочлена 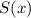 :
:
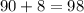
ответ: 98
Заметим, что
Подставим m=50, n=0 и получим:
То есть,
Так как
Это значит, что последняя цифра в десятичной записи числа
ответ: цифрой 1.