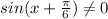
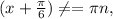 n∈Z
n∈Z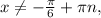 n∈Z
n∈Z
В решении.
Объяснение:
х - ширина прямоугольника.
у - длина прямоугольника.
ху = 27 (см²) - по условию задачи.
Р = 42 (см) - по условию задачи.
Периметр складывается из 2 длин и 1 ширины одного прямоугольника и 1 длины и 2 ширин другого прямоугольника, общая сторона = (у - х), получим выражение Р = 3у + 3х + (у - х).
Согласно условию, система уравнений:
ху = 27
3у + 3х + (у - х) = 42
Раскрыть скобки и привести подобные члены:
ху = 27
4у + 2х = 42
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 27/у
4у + 2*27/у = 42
4у + 54/у = 42
Умножить уравнение на у, чтобы избавиться от дробного выражения:
4у² + 54 = 42у
4у² - 42у + 54 = 0/4 для упрощения:
у² - 10,5у + 13,5 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =110,25 - 54 = 56,25 √D= 7,5
у₁=(-b-√D)/2a
у₁=(10,5-7,5)/2
у₁=1,5 ;
у₂=(-b+√D)/2a
у₂=(10,5+7,5)/2
у₂=18/2
у₂=9;
х = 27/у
х₁ = 27/у₁
х₁ = 27/1,5
х₁ = 18;
х₂ = 27/9
х₂ = 3;
Получили две пары решений: (18; 1,5) и (3; 9).
Так как по обозначению х - ширина, а у - длина, условию задачи соответствует вторая пара:
х = 3 (см) - ширина прямоугольника.
у = 9 (см) - длина прямоугольника.
Прямоугольники одинаковые, значения длины и ширины одинаковые.
Проверка:
3 * 9 = 27 (см²), верно.
3 * 9 + 3 * 3 + (9 - 3) = 27 + 9 + 6 = 42 (см), верно.
Второй вариант, где Р = 45 см.
х - ширина прямоугольника.
у - длина прямоугольника.
ху = 27 (см²) - по условию задачи.
Р = 45 (см) - по условию задачи.
Периметр складывается из 2 длин и 1 ширины одного прямоугольника и 1 длины и 2 ширин другого прямоугольника, общая сторона = (у - х), получим выражение Р = 3у + 3х + (у - х).
Согласно условию, система уравнений:
ху = 27
3у + 3х + (у - х) = 45
Раскрыть скобки и привести подобные члены:
ху = 27
4у + 2х = 45
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 27/у
4у + 2*27/у = 45
4у + 54/у = 45
Умножить уравнение на у, чтобы избавиться от дробного выражения:
4у² + 54 = 45у
4у² - 45у + 54 = 0/4 для упрощения:
у² - 11,25у + 13,5 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =126,5625 - 54 = 72,5625 √D= ≈ 8,5
у₁=(-b-√D)/2a
у₁=(11,25-8,5)/2
у₁= ≈ 1,375 ;
у₂=(-b+√D)/2a
у₂=(11,25+8,5)/2
у₂=19,75/2
у₂= ≈ 9,875;
х = 27/у
х₁ = 27/у₁
х₁ = 27/1,375
х₁ = ≈ 19,64;
х₂ = 27/9,875
х₂ = ≈ 2,73;
Получили две пары решений: (19,64; 1,375) и (2,73; 9,875).
Так как по обозначению х - ширина, а у - длина, условию задачи соответствует вторая пара:
х = ≈ 2,73 (см) - ширина прямоугольника.
у = ≈ 9,875 (см) - длина прямоугольника.
Прямоугольники одинаковые, значения длины и ширины одинаковые.
Проверка:
2,73 * 9,875 = ≈ 26,96 (см²) по условию задачи 27 (см²).
3 * 9,875 + 3 * 2,73 + (9,875 - 2,73) = 29,63 + 8,19 + 7,15 = ≈ 44,97 (см), по условию задачи 45 (см).
1)(3x^2-12)/(1-11x)>0
3(x^2-4)/(11(1/11-x))>0
3(x-2)(x+2)/(11(1/11-x))>0
+ - + -
(-2)(1/11)(2)
(-бескон.;-2)объединено(1/11;2)
2)243*(1/81)^{3x-2}=27^{x+3}
3^{5} *(3^(-4})^{3x-2}=(3^3)^{x+3}
3^{5} *3^{-12x+8}=3^{3x+9}
3^{5-12x+8}=3^{3x+9}
3^{13-12x}=3^{3x+9}
13-12x=3x+9
-12x-3x=9-13
-15x=-4
x=4/15
3)я не уверен, что ты правильно написал функцию проверь.
Мне кажется, что f(x)=1+8x-x^2, а не как у тебя 1+8-x^2
Решу для f(x)=1+8x-x^2
f`(x)=8-2x=2(4-x)
f`(x)=0 при 2(4-x)=0
4-x=0
х=4 принадлежит [2;5)
f(2)=1+8*2-2^2=1+16-4=13
f(4)=1+8*4-4^2=1+32-16=17-наибольшее значение
f(5)=1+8*5-5^2=1+40-25=16
4)2cos(x/2)+sqrt{2}=0
cos(x/2)=-sqrt{2}/2
x/2=pi- pi/4+2pi*n
x/2=3pi/4 +2pi*n |*2
x=6pi/4+4pi*n
x=3pi/2+4pi*n, n принадлежит Z
5)16^{x} -5*4^{x}=-4
(4^{x})^{2} -5*4^{x}+4=0 |t=4^{x}
t^2-5t+4=0
t1=1; t2=4
4^{x}=1 4^{x}=4^{1}
4^{x}=4^{0} x=1
x=0
ответ: 0;1
6) log_{\frac{1}{4}}\frac{3x+2}{2x-7}=-1
(3x+2)/(2x-7)=4
3x+2=4(2x-7)
3x+2=8x-28
3x-8x=-2-28
-5x=-30
x=6
Находим ОДЗ: (3х+2)/(2х-7)>0
3(x+2/3)/(2(x-3,5))>0
+ - +
(-2/3)(3,5)
(-бескон., -2/3) объединено(3,5;+бесконечность)
х=6 входит в область определения
ответ: 6
7)27^{x}<9^{x^2-1}
3^{3x}<3^{2x^2-2}
3x<2x^2 -2
2x^2 -3x-2>0
D=25
x1=2, x2=-1/2
8){x-y=7
{log-2(2x+y)=3
{x-y=7
{2x+y=8
y=8-2x
x-(8-2x)=7
x-8+2x=7
3x=15
x=5
y=8-2*5=-2
ответ:(5;2)
Подробнее - на -
Объяснение: