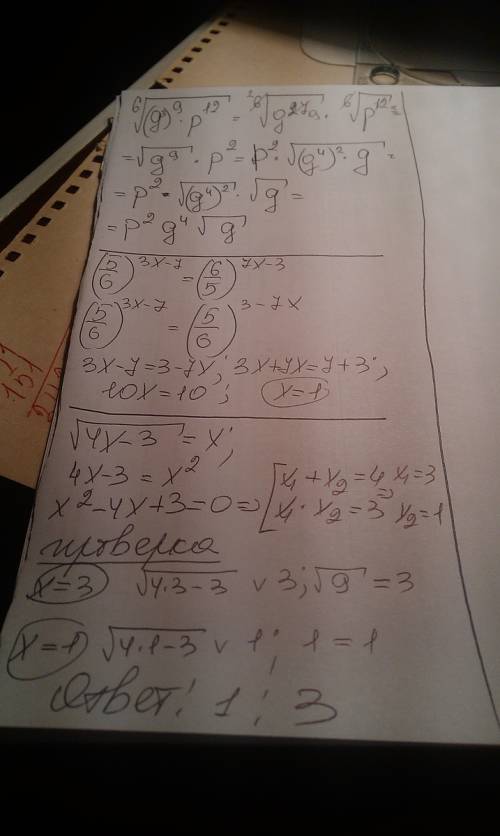
![1)\sqrt[6]{(g^3)^9p^{12}}=(g^{3*9}p^{12})^\frac{1}6=g^\frac{27}6p^\frac{12}6=g^\frac{9}2p^2=p^2\sqrt{g^9}\\\\2.a)(\frac{5}6)^{3x-7}=(\frac{6}5)^{7x-3}\\\\(\frac{6}5)^{-3x+7}=(\frac{6}5)^{7x-3}\\\\-3x+7=7x-3\\-10x=-10\\x=1\\\\2.b)\sqrt{4x-3}=x\\4x-3=x^2\\x^2-4x+3=0\\D=16-4*3=16-12=4\\\\x_1=\frac{4-2}2=1](/tpl/images/0407/1653/06370.png)
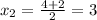
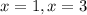
F - первообразная для f, если f = F'. Но так как производная от суммы - это сумма производных, и производная от числа равна нулю, то можно написать f = F' = (F+C)', где С - любое число.
То есть первообразная - это не какая-то одна функция, это класс функций. Для всех разных чисел С - будет разная первообразная F + C, и производная от каждой из них равна f.
У вас в задаче табличные вещи, поэтому гляньте в табличке первообразных.
В общем, первообразная будет
F(х) = 4x + sin(x) + C
Надо, что б если подставить вместо икса П/6, F получилась равной П.
sin(П\6) = 1/2, так как это синус 30 градусов
Получается равенство
П = 4*П\6 + 1\2 + С
6П = 4П+3 + 6С
С = (2П-3)\6
значит F = 4x + sin(x) + (2П-3)/6
а) На первое место можно использовать любую цифру из 5, на второе место - оставшиеся из 4 цифр, на третье место - оставшиеся 3 цифры, а на четвертое место - 2 цифры. По правилу произведения, четырехзначных чисел 5*4*3*2=120 можно составить
ответ: 120 чисел.
б) Так как на первое место 0 нельзя использовать, то берем любую цифру из 4, на второе место выбираем 4 цифры (0 используется), на третье место - оставшиеся 3 цифры, на третье место - 2 цифры. По правилу произведения, всего четырехзначных чисел 4*4*3*2=96
ответ: 96