Объяснение:
Постройте график функции у=6х-2.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -8 -2 4
Пользуясь графиком найдите:
1)значение функции если значение аргумента равно 2;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=2
у=6*2-2=10 при х=2 у=10
2)значение аргумента при котором значении функции равно - 2
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -2
-2=6х-2
-6х= -2+2
-6х=0
х=0 у= -2 при х=0
используем теорему Виета для решения всех заданий. Напомню, что по теореме Виета x1 + x2 = -p и x1 × x2 = q, где p и q коэффиценты уравнения x² + px + q = 0.
1. a) если корни равны 2 и 5, то p и q равны соответственно -7 и 10, подставляем их в исходное уравнение:
x² - 7x + 10 = 0, делаем все аналогично для пунктов б) и в):
б) x² - 2x -3 = 0
в) x² - 2,9x + 1 = 0
2. Подбором находим корни уравнений, затем делаем проверку:
а) 3; 2 3 × 2 = 6 и 3 + 2 = -(-5)
б) -3; -5 -3 × -5 = 15 и -3 - 5 = -8
в) 9; -1
г) 5; -2
д) 3; 14
е) 16; -5
3. Т.к. нам дан один корень, то можно найти второй через коэффицент q, а потом сделать проверку через коэффицент p:
a) 2 × x = -38, отсюда x = -19
проверим: -19 + 2 = -17, значит все правильно
б) поскольку это уравнение не приведенное, то разделим его на 7, чтобы сделать приведенным:
x² -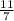 
- 
= 0
теперь мы можем сделать тоже, что и в пункте а):
2 × x =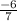
, отсюда х =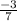 
проверим: 2 - 
=
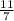
Все верно, значит мы решили правильно!
Cos 210 = Cos (180 + 30) = -Cos 30 = -√3/2
tg 240 = tg ( 270 - 30) = Ctg 30 = √3
√2/2 ·(-√3/2)·√3 = 3√2/4
Ctg 300 = Ctg (270 + 30) = - tg 30 = -1/√3
3√2 : (-1/√3) = -3√6/4
b) Сos 15 - Sin 15=√(1+Cos30)/2 - √(1 - Сos 30)/2=
=√(1+Сos 30)/√2 - √(1 + Cos 30)/√2 = (√(1 + √3/2) - √(1 - √3/2))/√2=
= (√(2 +√3) - √(2 - √3))/2
с)Sin²π/8 + Cos²3π/8 + Sin² 5π/8 + Cos² 7π/8 =
= Sin² π/8 + Cos ² 3π/8 + Sin² 3π/8 + Cos² π/8 = 1 + 1 = 2