В решении.
Объяснение:
Школьники занимаются прополкой огорода, который находится на пришкольном участке. Работают они с разной скоростью, а некоторые из них, как показывает практика, даже мешают общей работе, просто закапывая сорняки или перебрасывая их на участок соседа...
Вчерашняя работа показала, что Вася и Алина выпалывают гряду за 7 мин, Алина и Николай выпалывают её же за 14 мин, Николай и Вася — за 28 мин.
За сколько минут выполнят эту работу все вместе?
1 - гряда (условный объём работы).
1/7 - производительность Васи и Алины (часть гряды в минуту).
1/14 - производительность Николая и Алины (часть гряды в минуту).
1/28 - производительность Николая и Васи (часть гряды в минуту).
В + А + Н + А + Н + В = 1/7 + 1/14 + 1/28 = 1/4;
2(В + А + Н) = 1/4
Сократить (разделить) обе части уравнения на 2:
(В + А + Н) = 1/8 - общая производительность трёх школьников.
1 : 1/8 = 8 (минут).
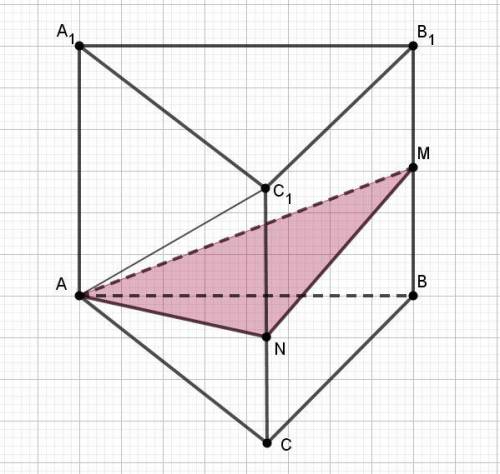
1) Сечение строится по заданным точкам.
Точку N находим в соответствии со свойством биссектрисы (см. пункт 2). Ребро СС1 точкой N делится в отношении 3:5.
2) По заданию AN является биссектрисой угла CAC1.
Диагональ АС1 боковой грани по Пифагору равна √(6² + 8²) = 10.
Примем СN = х.
По свойству биссектрисы х/6 = (8 - х)/10. Сократим знаменатели на 2.
24 - 3х = 5х,
8х = 24,
х = 24/8 = 3.
По заданию ВМ = 8/2 = 4.
Сечение AMN от призмы отсекает пирамиду с основанием BCNM, которое является трапецией (CN ║BM).
S(BCNM) =((3+4)/2)*6 = 21 кв.ед.
Высота H этой пирамиды равна высоте основания АВС.
H = 6*cos 30° = 6*√3/2 = 3√3.
V1 = V(ABCNM) = (1/3)*21*3√3 = 21√3 куб.ед.
Площадь основания призмы So = 6²√3/4 = 9√3 кв.ед.
Объём призмы V = 9√3*8 = 72√3 куб.ед.
Объём отсечённой части призмы равен V2 = 72√3 - 21√3 = 51√3 куб.ед.
ОтношениеV1/V2 = 21√3/51√3 = 7/17.
k=f`(x0)
f`(x)=-2x+b=9
2x=b-9
x=(b-9)/2>1
(b-9)/2 -1>0
(b-9-2)/2>0
2>0⇒b-11>0⇒b>11
b∈(11;∞)