надо найти уравнения этих касательных и точки их пересечения
f(x)=f(x0)+f`(x0)(x-x0)-общий вид касательной
1) для x0=-2
y`=0.5*2x+2=x+2
y`(-2)=-2+2=0
y(-2)=0.5*4+2*(-2)+2=2-4+2=0
тогда уравнение y1(x)=0+0(x+2); y1(x)=0
2)для нахождения касательных нужно определить точки касания, для этого в уравнение касательной я подставлю в y(x)=-4 и x=-1 (координаты точки А, так как она лежит на этих касательных тоже)
y(x)=y(x0)+(x0+1)(x-x0)
-4=y(x0)+(x0+2)(-1-x0)=0.5*x0^2+2x0+2-x0-x0^2-2-2x0
-4= -0.5x0^2-x0
0.5x0^2+x0-4=0
x0^2+2x0-8=9
D=4+32=36
x0=(-2+6)/2=2 и x0=(-2-6)/2=-4-это значит вторая касательная проходит через x0=-4 и x0=2
3)уравнение касательной через x0=-4
y2(x)=y(-4)+y`(-4)(x+4)=2-2(x+4)=2-2x-8; y2= -6-2x
y(-4)=0.5*16+2*(-4)+2=8-8+2=2
y(-4)=-4+2=-2
4) уравнение касательной с x0=2
y(x)=y(2)+y`(2)(x-2)=
y(2)=0.5*4+4+2=8
y`(2)=2+2=4
y3=8+4(x-2)=8+4x-8; y3=4x-уравнение третьей касательной
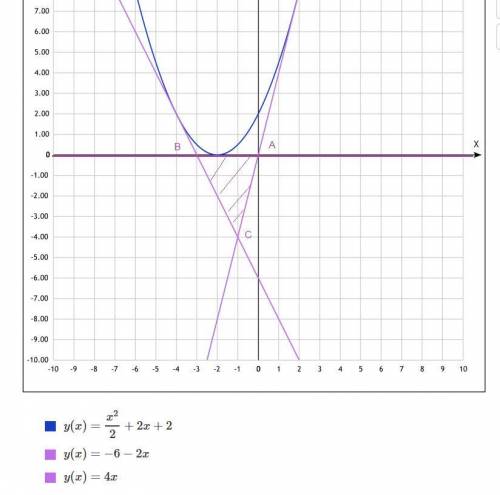
как видно из рисунка ( точки пересечения можно найти решая 3 три системы из 3 пар прямых касательных)
Площадь выделенного треугольника S=3*4/2=6
надо найти уравнения этих касательных и точки их пересечения
f(x)=f(x0)+f`(x0)(x-x0)-общий вид касательной
1) для x0=-2
y`=0.5*2x+2=x+2
y`(-2)=-2+2=0
y(-2)=0.5*4+2*(-2)+2=2-4+2=0
тогда уравнение y1(x)=0+0(x+2); y1(x)=0
2)для нахождения касательных нужно определить точки касания, для этого в уравнение касательной я подставлю в y(x)=-4 и x=-1 (координаты точки А, так как она лежит на этих касательных тоже)
y(x)=y(x0)+(x0+1)(x-x0)
-4=y(x0)+(x0+2)(-1-x0)=0.5*x0^2+2x0+2-x0-x0^2-2-2x0
-4= -0.5x0^2-x0
0.5x0^2+x0-4=0
x0^2+2x0-8=9
D=4+32=36
x0=(-2+6)/2=2 и x0=(-2-6)/2=-4-это значит вторая касательная проходит через x0=-4 и x0=2
3)уравнение касательной через x0=-4
y2(x)=y(-4)+y`(-4)(x+4)=2-2(x+4)=2-2x-8; y2= -6-2x
y(-4)=0.5*16+2*(-4)+2=8-8+2=2
y(-4)=-4+2=-2
4) уравнение касательной с x0=2
y(x)=y(2)+y`(2)(x-2)=
y(2)=0.5*4+4+2=8
y`(2)=2+2=4
y3=8+4(x-2)=8+4x-8; y3=4x-уравнение третьей касательной
как видно из рисунка ( точки пересечения можно найти решая 3 три системы из 3 пар прямых касательных)
Площадь выделенного треугольника S=3*4/2=6

Дискриминанты этих квадратных множителей равны