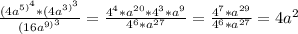
Алгебраическим выражением называется одна или несколько алгебраических величин (чисел и букв), соединенных между собой знаками алгебраических действий: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в целую степень (причём показатели корня и степени должны обязательно быть целыми числами) и знаками последовательности этих действий (обычно скобками различного вида). Количество величин, входящих в алгебраическое выражение, должно быть конечным.[1]
Пример алгебраического выражения:
«Алгебраическое выражение» — понятие синтаксическое, то есть нечто является алгебраическим выражением тогда и только тогда, когда подчиняется некоторым грамматическим правилам (см. Формальная грамматика). Если же буквы в алгебраическом выражении считать переменными, то алгебраическое выражение обретает смысл алгебраической функции.
Понятие алгебраического выражения можно дать и несколько иначе — это комбинация чисел, операторов, группировочных символов (скобок)) и/или свободных и связанных переменных, значение которых известно или может быть определено.