![\sqrt{4-2 \sqrt{2} } * \sqrt[4]{6+4 \sqrt{2} } = \sqrt{4-2 \sqrt{2} } * \sqrt[4]{(2+ \sqrt{2})^2 } =](/tpl/images/0407/6744/32617.png)
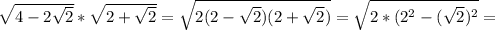
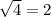
1) Неопределённость вида ∞/∞ . Предел частного многочленов при
х--> ∞ равен отношению старших коэффициентов, если многочлены равных степеней . Значит, в заданном примере в числитель можно записать любой многочлен второй степени со старшим коэффициентом, равным 2 .
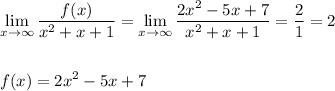
2) Неопределённость 0/0 . Многочлены раскладываются на множители , причём выделяется в обоих многочленах одинаковый множитель, который приводил к такой неопределённости . В данном примере это (х-1) . Затем он сокращается и неопределённость пропадает.
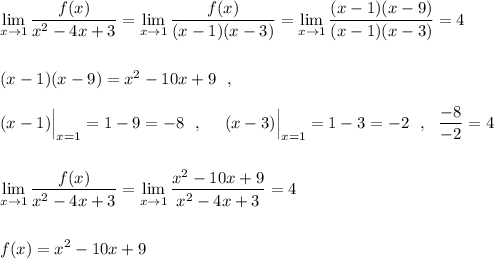
Відповідь:
Пояснення:
# Обидві нерівності рішаємо методом інтервалів .
13) [( x+ 4 )²( x² + 14x + 49 )]/( x + 5 ) ≥ 0 ;
[( x+ 4 )²( x + 7 )²]/( x + 5 ) ≥ 0 ; розглянемо функцію :
f( x ) = [( x+ 4 )²( x + 7 )²]/( x + 5 ) ;
f( x ) = 0 при х = - 7 і х = - 4 ;
f( x ) - невизначена при х = - 5 . Позначимо на числовій осі
f(- 8 ) < 0 ; f(- 6 ) < 0 ; f(- 4,5 ) > 0 ; f( 0 ) > 0 .
x Є {- 7 } U (- 5 ; + ∞ ) .
14) ( 2x + 3 )/( 3 - x ) ≥ ( x + 2 )/( x - 3 ) ;
( x + 2 )/( x - 3 ) + ( 2x + 3 )/( x - 3 ) ≤ 0 ;
( x + 2 + 2x + 3 )/( x - 3 ) ≤ 0 ;
( 3x + 5 )/( x - 3 ) ≤ 0 .
Розглянемо функцію :
f( x ) = ( 3x + 5 )/( x - 3 ) .
f( x ) = 0 при х = - 1 2/3 ;
f( x ) - невизначена при х = 3 . Позначимо на числовій осі
f(- 2 ) > 0 ; f( 0 ) < 0 ; f( 4 ) > 0 .
x Є [- 1 2/3 ; 3 ) .