а)

ОДЗ:у-любое число
б)

ОДЗ:у-любое число,кроме у≠9
у-9=0
у=9
в)

ОДЗ:у-любое число, кроме у≠3,у≠ -3
у²-9=0
(у-3)(у+3)=0
у-3=0 или у+3=0
у=3 у= -3
г)

ОДЗ:у-любое число
у²+3=0
у²≠ -3
ответ:уравнение не существует, квадрат числа не может быть отрицательным
д)
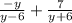
ОДЗ:у-любое число,кроме у≠6,у≠ -6
у-6=0 или у+6=0
у=6 у= -6
е)
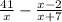
ОДЗ-х-любое число,кроме х≠0,х≠ -7
х=0 или х+7=0
х= -7
II варианта)
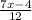
ОДЗ:х-любое число
б)
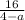
ОДЗ:а-любое число,кроме а≠4
4-а=0
-а= -4
а=4
в)
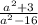
ОДЗ:а-любое число, кроме а≠4,а≠ -4
а²-16=0
(а-4)(а+4)=0
а-4=0 или а+4=0
а=4 а= -4
г)
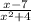
ОДЗ:х-любое число
х²+4=0
х²≠ -4
ответ:уравнение не существует, квадрат числа не может быть отрицательным
д)

ОДЗ:х-любое число,кроме х≠4,х≠ -4
х-4=0 или х+4=0
х=4 х= -4
е)
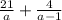
ОДЗ:а-любое число,кроме а≠0,а≠1
а=0 или а-1=0
а=1
ОДЗ-область допустимых значений
Cos x(2Sin x - 2) = 0
Cos x = 0 или 2Sin x - 2 = 0
x = π/2 + πk, k∈Z Sin x = 1
x = π/2 + 2πn , n ∈Z
Б) 1 - 2Sin² x + 3Sin x = 1
-2Sin² x + Sin x = 0
Sin x( - Sin x + 1) = 0
Sin x = 0 или - Sin x +1 = 0
x = πn , n∈Z Sin x = 1
x = π/2 + 2πk , k ∈Z
В) 4Cos³x - 3Cos x= Cos² x
4Cos³ x - 3Cos x - Cos² x = 0
Cos x( 4Cos² x - 3 - Cos x) = 0
Cos x =0 или 4Cos² x - Cos x - 3 = 0
x = π/2 + πk , k ∈Z Решаем как квадратное
D = 49
Cos x = 1 Cos x = - 3/4
x = 2πn , n∈Z x = +- arcCos(-3/4) + 2πm,m∈Z