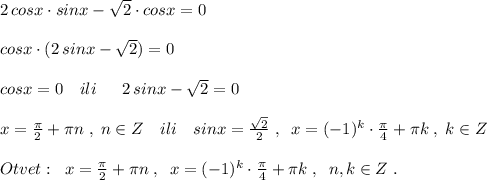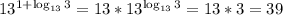
Если уравнение делить на cosx, то надо оговориться, что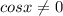 
, так как на 0 делить нельзя. В силу этого можно потерять корни уравнения, при которых cosx обращается в 0, это 
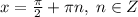. Тогда надо отдельно проверить, не являются ли 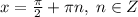корнями заданного уравнения, подставив их в это уравнение.
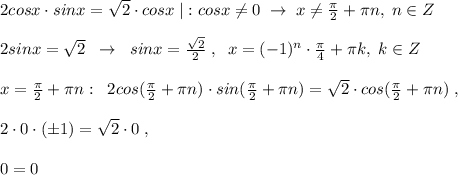
Так как получили верное равенство, то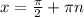 
являются корнями заданного уравнения.
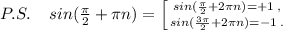
Чтобы не проводить лишнюю проверку , при решении уравнения надо просто вынести общий множитель cosx за скобку, тогда сразу получим две серии решений:
