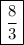квадратных единиц
Объяснение:
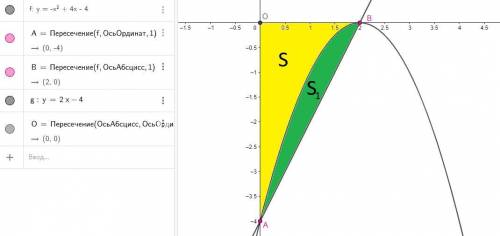
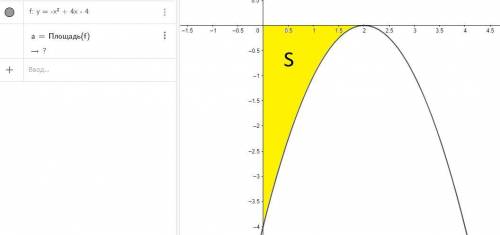
Построим график 
Пусть S площадь ограниченная графиком функции осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.
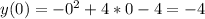
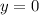
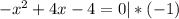
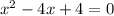
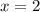
Координаты точек A и B:
A(0;-4)
B(2;0)
Пусть точка начало системы координат, тогда точка O имеет координаты O(0;0).
Узнаем уравнение прямой проходящей через точки A и B. Уравнение прямой с угловым коэффициентом в общем виде: 
.
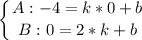
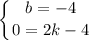
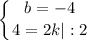
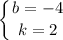
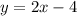
Пусть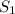 
- площадь между прямой 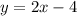и функцией
Пусть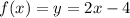 
и 
.
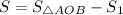
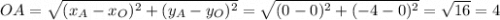
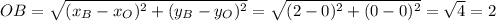
По формуле площади прямоугольного треугольника:
.
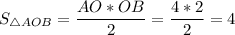Промежуток интегрирования: ![[0;2]](/tpl/images/4566/3708/2ae13.png)
Докажем, что 
при ![x \in [0;2]](/tpl/images/4566/3708/4a92d.png)
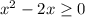
![x \in (-\infty;0] \cup [2;+\infty)](/tpl/images/4566/3708/254e2.png)
тогда можно сделать вывод, что
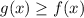при .
По теореме:
.
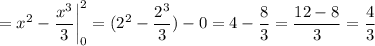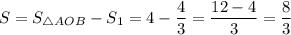квадратных единиц.
х=1+у
х-4у^2=1
х=1+у
1+у-4у^2=1
х=1+у
-4y^2+y=0
х=1+у
y(-4y+1)=0
х=1+у
y=0 или -4y+1=0
-4y=-1
y=1/4
а х=одна целая 1/4