Обозначим количество строк, в которых закрашена 1 клетка через a, а количество строк, в которых закрашены 7 клеток через b.
Обозначим количество столбцов, в которых закрашены 3 клетки через c, а количество столбцов, в которых закрашены 4 клетки через d.
Общее количество закрашенных красок N может быть выражено двояко:
N = a + 7b = 3c + 4d
Нам нужно найти min(N)
Имеются следующие ограничения и соотношения на a, b, c и d
a, b, c, d ∈ Z, 0 ≤ a,b,c,d ≤ 130, a + b = 130, c + d = 130
Подставим эти соотношения в равенство для N:
a + 7b = 3c + 4d
(a + b) + 6b = 3(c + d) + d
130 + 6b = 3 * 130 + d
d = 6b - 260
Т.к. 0 ≤ d ≤ 130, то:
0 ≤ 6b - 260 ≤ 130
260 ≤ 6b ≤ 390
43.(3) ≤ b ≤ 65
Т.к. нам нужно найти min(N) = min(a + 7b) = min(130 + 6b), то минимум достигается при минимальном b = 44.
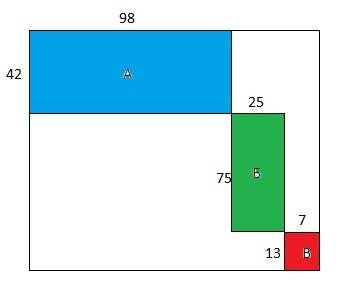
Осталось построить пример, показывающий, что возможна раскраска квадрата 130*130 так, что у него будет раскрашено по 7 клеток в 44 строках, по одной клетке в 86 (130 - 44) строках, по 4 клетки в 4 столбцах (6 * 44 - 260) и по 3 клетки в 126 столбцах (130 - 4), а всего 394 клетки (86 + 7 * 44).
Схема заполнения квадрата показана на рис.1 - будут заполнены только прямоугольники, размеры и расположение которых указаны.
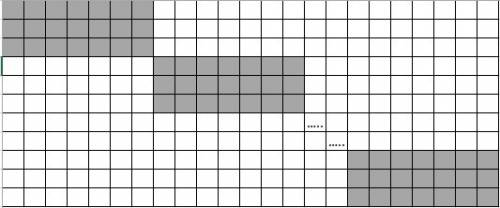
Прямоугольник А будет заполнен так, как указано на рис.2 - 14 блоков каждый размера 3 * 7.
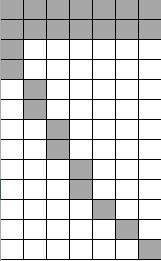
Прямоугольник Б будет заполнен так, как указано на рис.3 - 25 блоков каждый размера 3 * 1.
И наконец прямоугольник В заполнен так, как указано на рис. 3

сухой лист трепетал на ветках и, падая, крутился в воздухе, устилая колею пестрым ковром. он лежал в первой комнате на постели , подложив одну руку под затылок, а в другой держа погасшую трубку. женщины с детьми прятались, а мужчины ,схватив оружие, окружали белого человека, грозились убить. все в доме беспокоились, переходили к окнам и ,протаивая дыханием лед на стеклах, заглядывали на улицу. дядя яков, стоя на морозе в одной рубахе, тихонько посмеивался, моргая в синее холодное небо. чудовища шли медленно, обрывая молодые листья с верхушек пальм и папоротников ,по временам останавливаясь возле дерева, казавшегося особенно вкусным.
Последние цифры числа 3^n чередуются по правилу: 3,9,7,1,3,9,7,1...
Числа с цифрой 9 в конце происходят при n=4k-2, k-натуральные числа.
Тогда наше число n если существует имеет вид:
3^n+1=3^(4k-2)+1
Представим его так:
3^(4k-2)+1=(4-1)^(4k-2)+1
Выражение (4-1)^(4k-2) представляет собой многочлен бинома Ньютона. В нем каждый член кроме члена (-1)^(4k-2) помножен на какую либо степень четверки. Таким образом сумма всех членов кроме (-1)^(4k-2) делиться на 4 (Обозначим ее S). Тк 4k-2 cтепень четная при любом натуральном k,то
(-1)^(4k-2)=1
Тогда можно записать:
3^n +1=3^(4k-2)+1=4S+2
То есть число 3^n+1 при делении на 4 дает остаток 2. Но тк по предположению такое число делиться на 10^100 ,то как следствие должно делиться на 4 без остатка. То есть мы пришли к противоречию. То есть такого числа не существует.