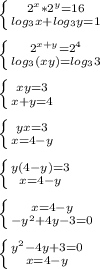
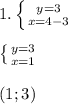
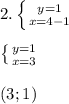
Пусть  - канонический базис в
- канонический базис в 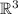 .
.
Тогда матрицу перехода 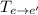 можно найти следующим образом:
можно найти следующим образом:
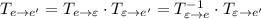
Если записать блочную матрицу 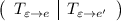 и привести путем элементарных преобразований к виду
и привести путем элементарных преобразований к виду  , то
, то 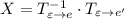
Матрицу 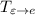 легко получить: достаточно записать в столбцы координаты векторов базиса
легко получить: достаточно записать в столбцы координаты векторов базиса  . Аналогично с матрицей
. Аналогично с матрицей 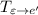 .
.
В итоге необходимо получить вид  следующей матрицы:
следующей матрицы:
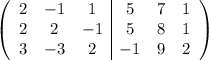
Вычтем первую строку из второй и третьей:
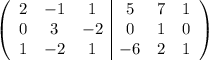
Вычтем из первой строки 2 третьих и поменяем их местами:
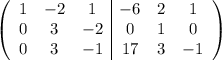
Вычтем из третьей строки вторую:
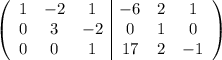
Прибавим ко второй строке 2 третьих и вычтем из первой третью:

Делим вторую строку на 3:
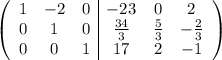
Прибавляем в первой строке 2 вторых:
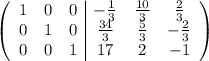
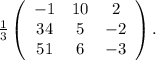
Событие A₁- " первая деталь имеет дефект"
Противоположное ему событие:
Â₁- " первая деталь не имеет дефекта"
Событие A₂- " вторая деталь имеет дефект"
Противоположное ему событие:
Â₂- " вторая деталь не имеет дефекта"
и так далее
до (N+3) cобытия
A(N+3)-" N+3-я деталь имеет дефект"
Â(N+3)-" N+3-я деталь не имеет дефекта"
a) A-" ни одна из деталей не имеет дефекта
A=Â₁∩Â₂·∩..∩Â(N+3)
б)В-"по крайней мере одна из деталей имеет дефект"
B=(A₁∩Â₂·∩..∩Â(N+3)∪Â₁∩А₂∩..∩Â(N+3)∪...∪Â₁∩Â₂∩..∩А(N+3))∪
∪(A₁∩А₂∩..∩Â(N+3)∪Â₁∩А₂∩А₃∩..∩Â(N+3)∪...∪Â₁∩Â₂...∩А(N+2)∩А(N+3))∪
∪...(A₁∩A₂·∩..∩A(N+3))
в)C-" только одна из деталей имеет дефект"
С=A₁∩Â₂·∩..∩Â(N+3)∪Â₁∩А₂∩..∩Â(N+3)∪...∪Â₁∩Â₂∩..∩А(N+3)
г) D-"не более двух деталей имеют дефект
Значит две, одна или ни одной:
D=(A₁∩А₂∩..∩Â(N+3)∪Â₁∩А₂∩А₃∩..∩Â(N+3)∪...∪Â₁∩Â₂...∩А(N+2)∩А(N+3))∪
(Это две1 и 2; 1и 3; ... предпоследняя и последняя)
∪(A₁∩Â₂·∩..∩Â(N+3)∪Â₁∩А₂∩..∩Â(N+3)∪...∪Â₁∩Â₂∩..∩А(N+3))∪
(Это одна; 1 или вторая 2или ... последняя)
∪(Â₁∩Â₂·∩..∩Â(N+3))
(это событие А - ни одна из деталь не имеет дефекта, все без дефекта)
log₃x+log₃y=1 log₃(x*y)=log₃3 x*y=3 x(4-x)=3 x²-4x+3=0 D=4
x₁=3 x₂=1
y₁=1 y₂=3.