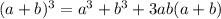
![\sqrt[3]{x-1} + \sqrt[3]{10-x} =3](/tpl/images/0408/4915/d71d0.png)
![( \sqrt[3]{x-1} + \sqrt[3]{10-x})^3 =3^3](/tpl/images/0408/4915/b283c.png)
![x-1+10-x+3 \sqrt[3]{(x-1)(10-x)} *( \sqrt[3]{x-1} + \sqrt[3]{10-x})=27](/tpl/images/0408/4915/8514b.png)
![\sqrt[3]{x-1} + \sqrt[3]{10-x} =3](/tpl/images/0408/4915/d71d0.png) , то
, то ![x-1+10-x+3 \sqrt[3]{(x-1)(10-x)} *3=27](/tpl/images/0408/4915/72e4f.png)
![9 \sqrt[3]{(x-1)(10-x)}=18](/tpl/images/0408/4915/90d0e.png)
![\sqrt[3]{(x-1)(10-x)}=2](/tpl/images/0408/4915/9dccb.png)
![( \sqrt[3]{(x-1)(10-x)})^3=2^3](/tpl/images/0408/4915/0b9ae.png)
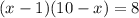
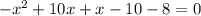
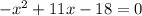
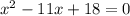

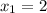
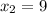
Решено верно :) надеюсь поймешь!
Объяснение:
Система решена точно правильно.
Получаем ответ: (4:5)
х=4 (1 слиток олова)
у=5 (1 слиток свинца)
Удачи, надеюсь
прощения за кривой почерк)
Система решена методом сложения.
Пояснение:
Ты должна в ОБОИХ уравнениях получить одинаковое число либо х либо у (я так решаю всегда).
В твоем случае я домножила 5у на -2у, а 2у на 5у.
Получили -10у и 10у! Обязательно должно быть одно отрицательное и одно положительное, чтобы их можно было убрать. (в твоем случае).
Ну, а дальше думаю, ты поняла)

х - 1 = 1 или х - 1 = 8
х = 2 или = 9
ответ: 2; 9.