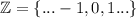
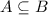 и
и 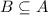
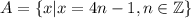
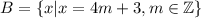


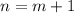
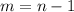
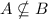 то,значит, есть такой элемент
то,значит, есть такой элемент 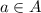 так что
так что 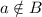 .
.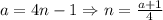
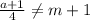
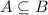
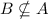 , то значит есть такой элемент
, то значит есть такой элемент 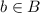 так что:
так что: 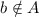
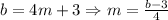
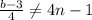
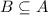
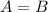
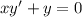
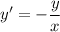 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными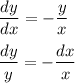
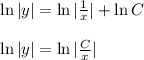
 - общее решение
- общее решение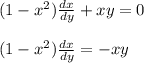

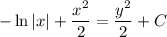 - общий интеграл
- общий интеграл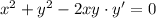

 , тогда
, тогда 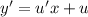



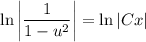
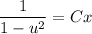
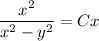 - общий интеграл
- общий интеграл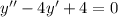
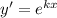 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
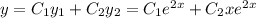 - общее решение
- общее решение
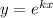 , тогда получаем
, тогда получаем
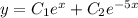

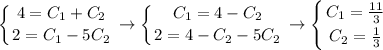
 - частное решение
- частное решение
25x² + 9 + 25x² - 7 - 2√(25х² + 9)√(25х² - 7) = 4
-2√(25х² + 9)√(25х² - 7) = -50x² +2
√(25х² + 9)√(25х² - 7) = 25x² -1 25 x² = t
√(t + 9)(t -7) = t -1 |²
(t + 9)( t - 7) = t² -2t +1
t² +2t -63 = t² -2t +1
4t = 64
t=16 ⇒ 25x² = 16⇒x² = 16/25⇒ х = +-4/5 = +-0,8