![\int {\frac{\sqrt[60]{arctg^{37} \, (x^4+5) }}{x^5 +10x +\frac{26}{x^3}}} \, dx = \int {\frac{x^3 \cdot arctg^{\frac{37}{60}} \, (x^4+5) }{x^8 +10x^4 +26}} \, dx=(*) \\ \\ t=arctg(x^4+5); \ \ dt = \frac{4x^3 \, dx}{1+x^8+10x+25}; \ \ dx= \frac{x^8 +10x+26 }{4x^3}\, dt \\ \\ (*) = \int {\frac{x^3 \cdot t^\frac{37}{60}}{x^8 +10x+26 } \cdot \frac{x^8 +10x+26 }{4x^3}\, dt =\frac{1}{4} \int {t^\frac{37}{60}} \, dt=\frac{1}{4 } \cdot \frac{60}{97} \cdot t^\frac{97}{60}+C}=](/tpl/images/0408/7029/9e62c.png)
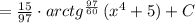
Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)