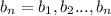
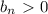
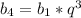
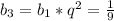 =>
=> 
 =>
=> 
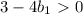

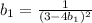
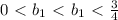 (*)
(*)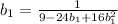
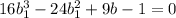
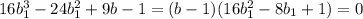
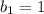 - посторонний корень (*)
- посторонний корень (*)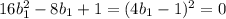
lim = 0
Объяснение:
Если разделить дробь на отдельные выражения, то их пределы будут равны +∞, следовательно, отношение выражений/дробь будет равно (+∞/+∞). Но эта дробь является неопределенной. Поэтому преобразуем эту дробь
lim(x→∞)((2x²-x+3)/(x³-8x+5)) →
→ ( lim(x→∞)( x³ ( 2/x - 1/x² + 3/x³ ) / lim(x→∞)( x³ ( 1 - 8/x² + 5/x³ ) )
Сокращаем и вычисляем пределы числителя и знаменателя:
lim(x→∞)(2/x-1/x²+3/x³) = lim(x→∞)(2*1/x-1/x²+3*1/x³) =
= 2*0-0+3*0 = 0
lim(x→∞)(1-8/x²+5/x³) = lim(x→∞)(1-8*1/x²+5*1/x³) =
= 1-8*0+5*0 = 1
0/1 = 0
Вроде так
lim = 0
Объяснение:
Если разделить дробь на отдельные выражения, то их пределы будут равны +∞, следовательно, отношение выражений/дробь будет равно (+∞/+∞). Но эта дробь является неопределенной. Поэтому преобразуем эту дробь
lim(x→∞)((2x²-x+3)/(x³-8x+5)) →
→ ( lim(x→∞)( x³ ( 2/x - 1/x² + 3/x³ ) / lim(x→∞)( x³ ( 1 - 8/x² + 5/x³ ) )
Сокращаем и вычисляем пределы числителя и знаменателя:
lim(x→∞)(2/x-1/x²+3/x³) = lim(x→∞)(2*1/x-1/x²+3*1/x³) =
= 2*0-0+3*0 = 0
lim(x→∞)(1-8/x²+5/x³) = lim(x→∞)(1-8*1/x²+5*1/x³) =
= 1-8*0+5*0 = 1
0/1 = 0
Вроде так