Строим угол C, равный данному углу Е. Для этого
строим луч СН;
проводим дуги с произвольным, но одинаковым радиусом с центрами в точках Е и С.;
D и F - точки пересечения дуги со сторонами угла Е, К - точка пересечения дуги с лучом СН;
проводим дугу с центром в точке F, радиусом FD, затем с тем же радиусом с центром в точке К. Точка пересечения дуг - L.
Проводим луч CL. Угол LCK равен данному углу Е.
На луче СН откладываем отрезок СА = b.
На луче CL откладываем отрезок СВ = а. Соединяем точки А и В.
Треугольник АВС - искомый.

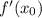 производная функции в данной точке. А
производная функции в данной точке. А  точка касания по иксу.
точка касания по иксу. мы должны найти производную общего типа этой функции.
мы должны найти производную общего типа этой функции.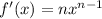 - где n это степень.
- где n это степень.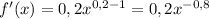


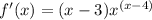
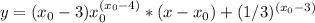
 и получаешь уравнение касательной.
и получаешь уравнение касательной.
Замена: tgx=t
Вернемся к замене:
1)
2)