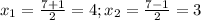
![\int (2x-3)\, dx=[t=2x-3\;,\; dt=d(2x-3)=(2x-3)'\, dx=2\, dx,\\\\dx=\frac{dt}{2}\, ]=\frac{1}{2}\cdot \int t\cdot dt=\frac{1}{2}\cdot \frac{t^2}{2}+C=\frac{1}{4}\cdot (2x-3)^2+C;\; \; \to \\\\\int _{-3}^2(2x-3)\, dx=\frac{1}{4}\cdot (2x-3)^2\, |_{-3}^2=\frac{1}{4}\cdot (1^2-(-9)^2)=\\\\=\frac{1}{4}\cdot (1-9)=-2](/tpl/images/0624/4857/fe06b.png)
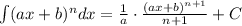
(-∞; -3)∪(1; 10)
Объяснение:
Решаем неравенство
(x+3)·(x-1)·(x-10)<0
методом интервалов:
1) Определим нули левой части неравенства, то ест решаем уравнение (x+3)·(x-1)·(x-10)=0:
x+3=0 ⇔ x = -3
x-1=0 ⇔ x = 1
x-10=0 ⇔ x = 10
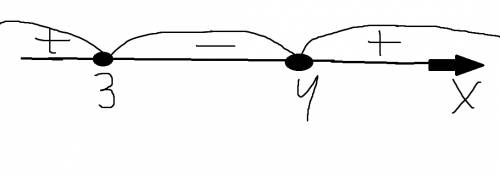
2) Нули левой части делит ось Ох на следующие промежутки, в которых знак выражения (x+3)(x-1)(x-10) не меняется:
(-∞; -3), (-3; 1), (1; 10), (10; +∞).
3) Определим знаки выражения в каждом промежутке:
а) x∈(-∞; -3): (x+3)·(x-1)·(x-10)<0, например при x= -100:
(-5+3)·(-5-1)·(-5-10)= -180<0;
б) x∈(-3; 1): (x+3)·(x-1)·(x-10)>0, например при x= 0:
(0+3)(0-1)(0-10)=30>0;
в) x∈(1; 10): (x+3)·(x-1)·(x-10)<0, например при x= 2:
(2+3)·(2-1)·(2-10)= -40<0;
г) x∈(10; +∞): (x+3)·(x-1)·(x-10)>0, например при x= 11:
(11+3)·(11-1)·(11-10)= 140>0;
4) Решением неравенства будет множество:
(-∞; -3)∪(1; 10).
+ 3 - 4+
ответ (-00,3]U[4,+00)