Объяснение:
Действуем по такому методу:
Если знаменатель дроби — квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на сопряженный на квадратный корень, находящийся в знаменателе (это, конечно, не всегда, точнее сказать, надо умножить на такое число, чтобы при перемножении знаменателя с ним убирался корень)
1) 
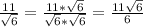
2) 
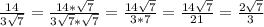
3)
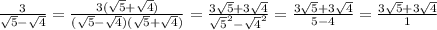вот здесь, как раз-то число, на которое умножаем, это не совсем знаменатель, но именно при перемножении с ним, мы можем избавиться от иррациональности.
P.S. если решил правильно, отметь как лучший)
x-27=0⇒x=27∈[23;40]
y(23)=-4e^5
y(27)=0
y(40)=13e^(-12) наиб