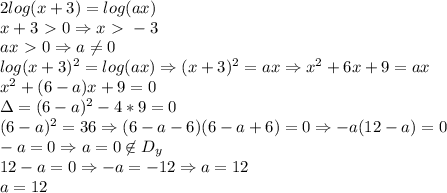
Пусть х =производительность (л/мин) 1-й трубы, тогда (х+5) -производительность 2-й трубы. 1-я труба заполняет резервуар 400л за время (400/х). 2-я труба заполняет резервуар 900л за время 900/(х+5). 2ч20мин = 140мин
Уравнение: 400/х - 900/(х+5) = 140
разделим на 20
20/х - 45/(х+5) = 7
20(х+5) - 45х = 7х(х+5)
20х + 100 - 45х = 7х² +35х
7х² + 60х - 100 = 0
D = 60² + 28·100 = 3600 + 2800 = 6400
√D = 80
x₁ = (-60 + 80):14 = 10/7
x₂ = (-60 - 80):14 = -10 (не является решением, т.к. производительность не может быть отрицательной)
ответ: 10/7 л/мин
Пример №1 (б):
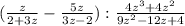
(в скобках приведем разность и вычитаемое к общему знаменателю)
(дробь за скобкой перевернем, заменив тем самым деление на умножение)
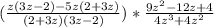
(раскроем скобки)
(в дроби за скобкой числитель свернем по формуле квадрата разности, а в знаменателе этой дроби вынесем общий множитель 4z^2 за скобку)
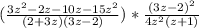
(приведём подобные в числителе первой дроби)
(сократим в знаменателе первой дроби (3z-2) и в числителе второй дроби (3z-2))
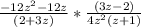
(в числителе первой дроби вынесем общий множитель -12z за скобку)
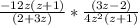
(сократим -12z в числителе первой дроби и 4z^2 в знаменателе второй дроби на 4z)
(сократим (z+1) в числителе первой дроби и (z+1) в знаменателе второй дроби)
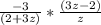
(раскроем скобки в числителе и знаменателе дроби соответственно)
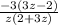
(раскроем скобки)
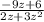
ответ: 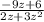
Пример №2 (в):
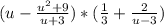
(в первой скобке приведем две дроби к общему знаменателю)
(во второй скобке приведем две дроби к общему знаменателю)
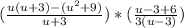
(раскроем скобки и приведем подобные в числителе первой дроби)
(приведем подобные в числителе второй дроби)
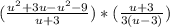
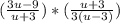
(вынесем общий множитель 3 в числителе первой дроби)
(сократим знаменатель первой дроби (u+3) и числитель второй дроби (u+3))
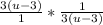
(сократим числитель первой дроби и знаменатель второй дроби на 3)
(сократим (u-3) в числителе первой дроби и (u-3) в знаменателе второй дроби)
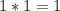
ответ: 1
D=(6-a)²-4·9=36-12a+a²-36=a²-12a
Квадратное уравнение имеет одно решение, если дискриминант равен 0
a²-12a=0
a(a-12)=0
a=0 или a=12
при a=0 правая часть уравнения не имеет смысла
ответ При а=12