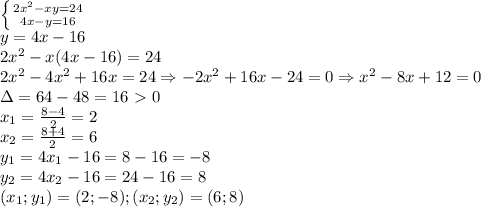
(x - 2)(x ^ 2 + |x - 1|) - x ^ 2 + 2x = 0 x ^ 3 + x|x - 1|- 2x ^ 2 - 2x| * x - 1| - x ^ 2 + 2x = 0 x ^ 3 + x
x|x - 1|- 3x ^ 2 - 2x| * x - 1| + 2x = 0 x ^ 3 + x
x * (x - 1) - 3x ^ 2 - 2(x - 1) + 2x = 0,
x - 1 >= 0 x ^ 3 + x(- (x - 1)) - 3x ^ 2 - 2x * (- (x - 1)) + 2x = 0
x - 1 < 0 x = 2 x = - 1,
x >= 1 x = 1 х = 1 х = 2 ,
X <1 x = 1 x = 2 x
x = 1 x = 2 Рішення x 1 =1,x 2 =2
x/(x + 5) - (1x + 51)/(5 - x) = 50/(x ^ 2 - 25) x/(x + 5) - (1x + 51)/(5 - x) = 50/(x ^ 2 - 25), x = - 5, x = 5 x/(x + 5) - (x + 51)/(5 - x) = 50/(x ^ 2 - 25) x/(x + 5) - (x + 51)/(5 - x) * 50/(x ^ 2 - 25) = 0 x/(x + 5) * (x + 51)/(- (x - 5)) * 50/((x - 5)(x + 5)) - 0 x/(x + 5) + (x + 51)/(x - 5) - 50/((x - 5)(x + 5)) = 0 (x(x - 5) + (x + 5)(x + 51) - 50)/((x - 5)(x + 5)) = 0 (x ^ 2 - 5x + x ^ 2 + 51x + 5x + 255 - 50)/((x - 5)(x + 5)) = 0 (2x ^ 2 + 41x + 10x + 205)/((x - 5)(x + 5)) = 0 (x(2x + 47) + 5(2x + 47))/((x - 5)(x + 5)) = 0 ((2x + 41)(x + 5))/((x - 5)(x + 5)) = 0 (2x + 41)/(x - 5) = 0 2x + 41 = 0 2x = - 41 x=- 41 2 ,x=-5.x=5 Рішення x = - 41/2 Альтернативна форма 1 1 x = - 20 - x=-20 5
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 
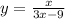. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б) 
при 
Если x = -5, то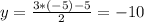 
Если х= 3, то 
Значит, 
2x²-4x²+16x-24=0
-2x²+16x-24=0 |:(-2)
x²-8x+12=0
D= 64 - 48 = 16
x₁= 8+4/2=6
x₂=8-4/2 = 2
y₁= 4*6-16 = 8
y₂= 4*2-16= -8
ответ: (6;8), (2;-8).