-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
1. -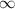 до
до 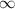
2, 3sin(-x/2)=-3sin(x/2)-нечетная
3, OY-0
OX-2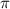 n
n
4. От 0 до 2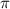 n-положит
n-положит
от 2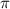 до 4
до 4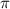 n -отрицательный
n -отрицательный
5, Точка y=3
6.От -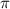 до
до 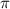 n - возрастает
n - возрастает
от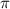 до 3
до 3 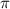 n- убывает
n- убывает
7.это синусоида , растянутая вверх до точки 3 и расширенная до 2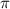 вместо
вместо 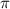 .
.