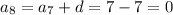Можно взять 7 или 8 членов прогрессии
Объяснение:
Дано:
a₂ + a₄ + a₆ = 84
a₄ · a₇ = 196
Sn = 196
Найти:
n
а₁ + d + a₁ + 3d + a₁ + 5d = 84
(a₁ + 3d)(a₁ + 6d) = 196
3a₁ + 9d = 84
a₁² + 9a₁d + 18d² = 196
a₁ = 28 - 3d
(28 - 3d)² + 9d(28 - 3d) + 18d² = 196
784 - 168d + 9d² + 252d - 27d² + 18d² = 196
84d + 588 = 0
84d = - 588
d = -7
a₁ = 28 - 3 (-7) = 49
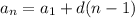
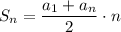
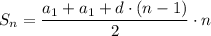
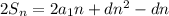
2 · 196 = 2 · 49n - 7n² + 7n
7n² - 105 n + 392 = 0
n² - 15n + 56 = 0
D = 225 - 224 = 1
n₁ = 0.5(15 - 1) = 7
n₂ = 0.5(15 + 1) = 8
можно взять 7 членов прогрессии
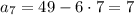
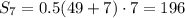
а можно взять и 8 членов прогрессии, так как