Объяснение:
Проверим случай p=5, уйдет квадратичная часть, но линейная останется, значит неравенство не будет выполняться для всех x.
При p не равном 5 график левой части неравенства представляет собой параболу, для того, чтобы неравенство было верно для любого x вся парабола должна лежать ниже оси абсцисс, т. е. ветви вниз(p-5<0) и D(дискриминант)<0.
D1=(2p-4)^2-4(p-5)(-p-3)=8p^2-24p-44<0
2p^2-6p-11<0
D2=36+88=124
p1=(3-sqrt(31))/2
p2=(3+sqrt(31))/2
D1<0 при
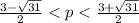
Эти значения p меньше пяти(т.е. ветви направлены вниз). Заносим их в ответ.
Всего возможных исходов 6^3, поскольку для каждого из чисел a, b, c есть по 6 вариантов. Остается посчитать число благоприятных исходов.
1) a можно выбрать произвольно - шестью остается только 5 вариантов (нельзя, чтобы совпал с тем, что уже выбрано для a), с - 4 варианта. Всего 6 * 5 * 4 благоприятных исходов.
Вероятность P = число благоприятных исходов / общее возможное число исходов
P(A) = 6 * 5 * 4 / 6^3 = 5 * 4 / 6^2 = 5/9
2) Благоприятен только один исход, а именно (6, 6, 6).
P(B) = 1 / 6^3 = 1/216
3) Можно заметить, что это событие дополняет B, тогда сумма вероятностей P(B) + P(C) должна быть равна единице.
P(C) = 1 - 1/216 = 215/216
ответ. P(A) = 5/9, P(B) = 1/216, P(C) = 215/216