(Х) км/ч-время на первой части пути;
(Х+15) км/ч - время на второй части пути;
(24/х) ч-скорость на первой части пути;
(36/(x+15)) ч - скорость на второй части пути;
4 км/ч - разница между первой и второй скоростью
Составляем и решаем уравнение:
36/(x+15)-24/x=4
Находим общий знаменатель, подписываем дополнительные множители, приводим к квадратному. (-4x^2-24x+384=0)
Находим корни уравнения: x1=6; x2=-16 (не удовлетворяет условию)
х-время на первой части пути, значит, время на первой части пути = 6 ч.
Находим скорость: 24/6=4
ответ: 4 км/ч
касателная ест производной функции в точке.
производная :
(3+5x+3x²)' = (3)'+(5x)'+(3x²)' = 0 + 5 + 3 · 2x = 6x + 5
искаем аргументу для которрого 6x + 5 = (-7)
6x =( -7 ) -5 = -12
x= (-2)
тепер найдем значение функцйии для этого аргумента
y= 3+5x+3x² где x = (-2)
y= 3 + 5 · (-2) + 3 · (-2)² = 3 + (-10) + 3· 4 = (-7) + 12= 5
искана точка, т= ((-2) , 5 )
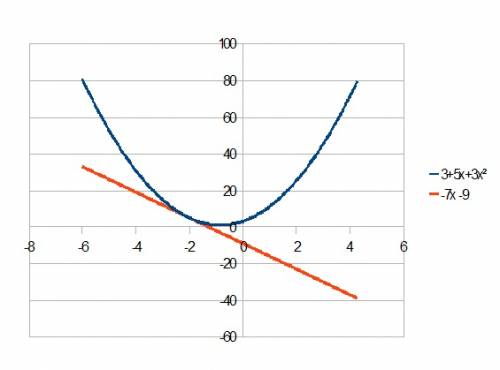
во вложению граф,
касателная y = (-7) x + C по поводу grafa найдем число C
5 = (-7)· (-2)+ C
C= 5 - 14 = -9
касателна в точке (-2, 5) : y= (-7) x - 9
извините лексикальное граматические ошибки я не русский
a^3 + b^3 = c^3 + d^3
Разложим сумму кубов слева и справа
(a + b)(a^2 - ab + b^2) = (c + d)(c^2 - cd + d^2)
Известно, что a + b = c + d, разделим на них
a^2 - ab + b^2 = c^2 - cd + d^2
Выделим полные квадраты
a^2 + 2ab + b^2 - 3ab = c^2 + 2cd + d^2 - 3cd
(a + b)^2 - 3ab = (c + d)^2 - 3cd
Опять-таки, a + b = c + d, значит, (a + b)^2 = (c + d)^2, вычтем их
-3ab = -3cd
ab = cd
Вернемся к равенству:
a^2 - ab + b^2 = c^2 - cd + d^2
Если ab = cd, то прибавим их
a^2 + b^2 = c^2 + d^2
Что и требовалось доказать