1/2 больше чем 1/3, но корень из 204 больше 496
корень из 204 это примерно 14,3527, а корень 496-22, 27
1/2*14,3527=7,175, а 1/3*22,27=7,42
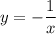и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
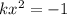и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
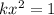и при k<0 это уравнение решений не имеет.
, имеем
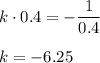
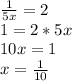
1/2√204 и 1/3 √495
Запишем их так.
(√204)/2 и (√495)/3 (А так можно? Да, можно.)
Приведем к общему знаменателю.
(3*√204)/6 и (2*√495)/6 (Что за непонятная * ? Это знак умножения)
Внесем под корень числа
(√1863)/6 и (√ 1980)/6
Теперь видно, что первая дробь, меньше второй дроби.
(√1863)/6 < (√ 1980)/6