 натуральное число, тогда
натуральное число, тогда 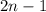 будет натуральным и нечётным числом. Возведем данное число в квадрат:
будет натуральным и нечётным числом. Возведем данное число в квадрат: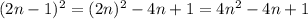

 , 0 делиться на 8, следовательно условие выполняется.
, 0 делиться на 8, следовательно условие выполняется. . Докажем что данное число делиться на 8 при
. Докажем что данное число делиться на 8 при 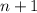 :
:
 делиться на 8. Следовательно, существует натуральный
делиться на 8. Следовательно, существует натуральный 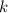 так что:
так что: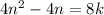
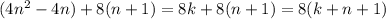 следовательно, при
следовательно, при 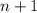 данное число тоже делиться на 8. Ч.Т.Д.
данное число тоже делиться на 8. Ч.Т.Д.
 натуральное число, тогда
натуральное число, тогда 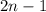 будет натуральным и нечётным числом. Возведем данное число в квадрат:
будет натуральным и нечётным числом. Возведем данное число в квадрат: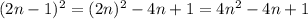

 , 0 делиться на 8, следовательно условие выполняется.
, 0 делиться на 8, следовательно условие выполняется. . Докажем что данное число делиться на 8 при
. Докажем что данное число делиться на 8 при 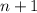 :
:
 делиться на 8. Следовательно, существует натуральный
делиться на 8. Следовательно, существует натуральный 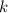 так что:
так что: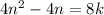
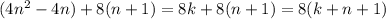 следовательно, при
следовательно, при 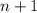 данное число тоже делиться на 8. Ч.Т.Д.
данное число тоже делиться на 8. Ч.Т.Д.
12 *2 = 24
10+ ( -2 ) =8
24 : 8 = 3 - верно
(2+6 ) * 3 = 24
28 6 = 12
24 : 12 = 2 - верно