Question

Не просто решите, а объясните ход своих мыслей. просто решение мне не нужно.

Answer 1

Нам известен котангенс, а требуют найти тангенс. Попробуем преобразовать этот тангенс так, чтобы в нём встречался котангенс.

Что можно сделать с тангенсом суммы? Разложить по формуле:

$tg(2\alpha+\frac{5\pi}{4})=\frac{tg2\alpha+tg\frac{5\pi}{4}}{1-tg2\alpha*tg\frac{5\pi}{4}}=\frac{tg2\alpha+1}{1-tg2\alpha}$

Получили тангенсы, но двойного угла. Разложим их тоже:

$\frac{tg2\alpha+1}{1-tg2\alpha}=\frac{\frac{2tg\alpha}{1-tg^2\alpha}+1}{1-\frac{2tg\alpha}{1-tg^2\alpha}}=\frac{\frac{2tg\alpha+1-tg^2\alpha}{1-tg^2\alpha}}{\frac{1-2tg\alpha-tg^2\alpha}{1-tg^2\alpha}}=\frac{2tg\alpha+1-tg^2\alpha}{1-2tg\alpha-tg^2\alpha}$

Если сейчас заменить тангенсы на котангенсы, нам придётся работать с трёхэтажными дробями, поэтому лучше выразим тангенс из котангенса и будем подставлять: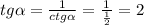 $tg\alpha=\frac{1}{ctg\alpha}=\frac{1}{\frac{1}{2}}=2$

И теперь подставим двойку вместо тангенсов:

$\frac{2tg\alpha+1-tg^2\alpha}{1-2tg\alpha-tg^2\alpha}=\frac{2*2+1-2^2}{1-2*2-2^2}=\frac{1}{-7}=-\frac{1}{7}$

ответ: 5)

Answer 2

я бы делал так:

1) tg α*Ctg α = 1, ⇒ tg α = 2

2) tg2α = 2tgα/(1 - tg²α) = 4/(1 - 4) = -4/3

3) tg(2α + 5π/4) = (tg2α + tg5π/4)/(1 - tg2α*tg5π/4)

осталось подставить  все известные величины  и решить получившийся пример.

(-4/3 +1)/(1 +4/3*1) = -1/7