условно сходится
Объяснение:
Для выяснения сходимости ряда используем признак Лейбница.
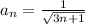
Очевидно, что
1. 
, так как с увеличением номера n увеличивается знаменатель, а с ростом знаменателя дробь становится все меньше и меньше;
2.
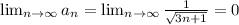
Надеюсь, данный факт ясен.
Два условия выполнены, следовательно, ряд по признаку Лейбница сходится.
Выясним вопрос относительно абсолютной сходимости. Для этого нужно рассмотреть соответствующий ряд из модулей исходного ряда.
Напомню, что модуль "съедает" множитель вида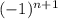 
. Значит, общий член нового ряда имеет вид 
.
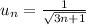Для установления сходимости данного ряда используем интегральный признак Коши. Это можно сделать, поскольку действительнозначная функция
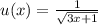
неотрицательна, непрерывна и убывает на интервале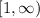 
Можно рассмотреть несобственный интеграл. Исследуем его на сходимость. подробности в приложенном файле.
Итак, получена бесконечность, стало быть, несобственный интеграл расходится.
Ряд сходится либо расходится вместе с несобственным интегралом. То есть, расходится.
Таким образом, сам ряд сходится. Но ряд из модулей расходится, что исключает абсолютную сходимость ряда. А сходящийся ряд, не сходящийся абсолютно, сходится условно.
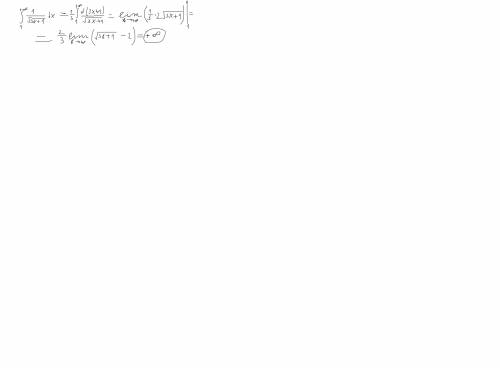
ответ: 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).
Объяснение:
Запишем данный многочлен в виде 2*(x³+5/2*x²+1/2*x-1). Для того, чтобы разложить многочлен в скобках на множители, нужно решить уравнение x³+5/2*x²+1/2*x-1=0. Это - приведённое кубическое уравнение, поэтому одним из его целых корней (если они есть) может быть целый делитель свободного члена данного уравнения, то есть числа -1. Таких делителей всего два: 1 и -1. Подставляя значения x=1 и x=-1 в данное уравнение, находим, что число x=1 не является корнем уравнения, а число x=-1 - является. Теперь разделим многочлен x³+5/2*x²+1/2*x-1 на двучлен x-(-1)=x+1. После этого получим тождество x³+5/2*x²+1/2*x-1=(x+1)*(x²+3/2*x-1). Теперь разложим на множители квадратный трёхчлен x²+3/2*x-1, для чего нужно решить уравнение x²+3/2*x-1=0. Оно имеет корни x1=1/2 и x2=-2, поэтому x²+3/2*x-1=0=(x-1/2)*(x+2). Тогда x³+5/2*x²+1/2*x-1=(x+1)*(x-1/2)*(x+2) и окончательно 2*x³+5*x²+x-2=(x+1)*(x+2)*(2*x-1).
короче, ответ - -2/5