Чтобы построить график линейной функции - прямую линию - нужны две точки на координатной плоскости.
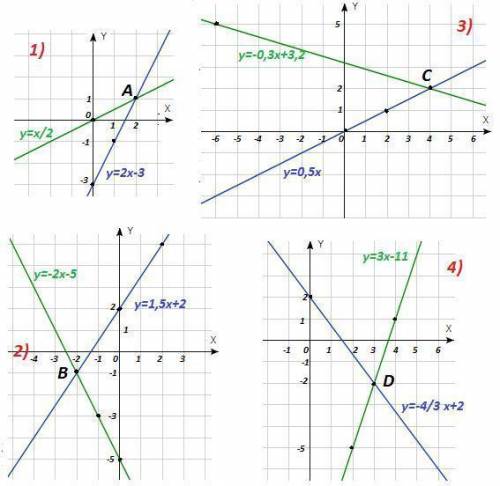
1) y = 2x - 3; y = 1/2 x
x | 0 1 x | 0 2
y | -3 -1 y | 0 1
Точка пересечения A(2; 1)
2) y = 1,5x + 2; y = -2x - 5
x | 0 2 x | 0 -1
y | 2 5 y | -5 -3
Точка пересечения B(-2; -1)
3) y = 0,5x ; y = -0,3x + 3,2
x | 0 2 x | 4 -6
y | 0 1 y | 2 5
Точка пересечения C(4; 2)
4) y = -4/3 x + 2; y = 3x - 11
x | 0 3 x | 2 4
y | 2 -2 y | -5 1
Точка пересечения D(3; -2)
Объяснение:
1)
1-(8a-3)²=1-(64а²-48а+9)=1-64а²+48а-9=-64а²+48а+(1-9)=-64а²+48а-8=-8(x-0,25)(x-0,5)=-(8х-2)(8х-4)=(2-8х)(8х-4)
Для того чтобы разложить на множители нужно приравнять данное выражение к нулю
-64а²+48а-8=0
Cчитаем дискриминант:
Дискриминант положительный
2) a⁵+a⁴-2a³-2a²+a+1