Считать будем все броски подряд, из которых нечетные (1, 3, 5) делает первый игрок, а четные (2, 4, 6) - второй.
Первый побеждает в следующих ситуациях:
- попал 1 броском
- попал 3 броском, а все предыдущие броски закончились промахом
- попал 5 броском, а все предыдущие броски закончились промахом
Второй побеждает в следующих ситуациях:
- попал 2 броском, а предыдущий бросок закончился промахом
- попал 4 броском, а все предыдущие броски закончились промахом
- попал 6 броском, а все предыдущие броски закончились промахом
Зная вероятность попадания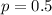 
, вычислим вероятность промаха:
:
Вероятность победы первого игрока:
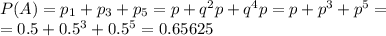
Вероятность победы второго игрока:
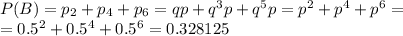
ответ: победа первого с вероятностью 0.65625, победа второго с вероятностью 0.328125
(1; 4); (4; 1)
Объяснение:
{ x√x + y√y = 9
{ x√y + y√x = 6
Переходим к новым переменным
a = √x; x = a^2; x√x = a^3
b = √y; y = b^2; y√y = b^3
{ a^3 + b^3 = 9
{ a^2*b + ab^2 = 6
Умножим второе уравнение на 3
{ a^3 + b^3 = 9
{ 3a^2*b + 3ab^2 = 18
Складываем уравнения
a^3 + b^3 + 3a^2*b + 3ab^2 = 9 + 18
Слева записан куб суммы
(a + b)^3 = 27
a + b = 3
b = 3 - a
Подставляем
a^2*(3 - a) + a(3 - a)^2 = 6
a(3 - a)(a + 3 - a) = 6
3a(3 - a) = 6
a(3 - a) = 2
-a^2 + 3a = 2
a^2 - 3a + 2 = 0
(a - 1)(a - 2) = 0
1) a = 1; b = 2
x = a^2 = 1; y = b^2 = 4
(1; 4) - это решение.
2) a = 2; b = 1
x = a^2 = 4; y = b^2 = 1
(4; 1) - это решение.
(x² +2x -x² +x -3x+3)/(x(x-1)) =3/(x(x-1)) .
2) (a³ +3)/a³ -(3-a)/3a = 1+3/a³ -1/a+1/3=4/3 +(3-a²)/a³.
или по другому :
( 3(a³+3) -(3-a)a² )/3a³ =(3a³ +9 -3a²+a³)/3a³ =(4a³ +3(3-a²))/3a³ =4/3 + (3-a²))/a³.
3) 18x³/(7*b^4 )*14b/9x² = (18x³ *14b)/(7*(b^4)*9x²)= 2x/b³.