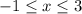или ![x \in [-1;3]](/tpl/images/1416/7689/cd001.png)
Объяснение:
Модуль раскрывается двумя вариантами: со знаком + или со знаком - . В этой задаче 2 модуля, следовательно максимум может быть 4 раскрытия.
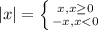
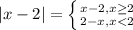
На практике имеем 3 области:
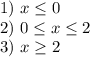
Область 
не существует, т.к. нет пересечений у неравенств, задающих область.
Рассмотрим каждый из трех случаев:
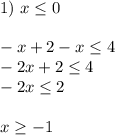
Получили решение, лежащее в области: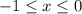 
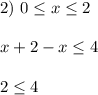
Получили неравенство, выполненное для любого x из этой области. Следовательно решение в этой области - сама область: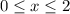 
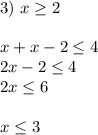
Получили решение, лежащее в области: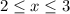 
"Сшиваем" полученные решение и получаем:
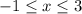или
в учебник загляни ТЕОРЕМЫ посмотри и узнаешь всё что надо!1Пусть при пересечении прямых а и с секущей АВ накрест лежащие углы 1 и 2 равны. Если углы 1 и 2 прямые, то прямые а и с перпендикулярны к прямой АВ и следовательно параллельны. Доп. Построен. Провелем перпендикуляр ОН из середины отрезка АВ к прямой а. На прямой с от точки В отложим отрезок ВН1, равный отрезку АН и проведем отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними. Поэтому угол 3=4 и 5=6. Из равенства 3=4, точки Н, Р и Н1 лежат на одной прямой, а из равенства 5=6 : угол 6 прямой. прямые а и с перпенликулярны к прямой НН1, поэтому они параллельны. :-)
3Пусть при пересечении прямых а и b секущей c сумма односторонних углов равна 180. Т.к. эти углы 3 и 4 смежные, то 3+4=180. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые параллельны.
4те, которые не требуют доказательств.
пример: параллельные линии не пересекаются
или
АКСИОМА – принцип или положение, принимаемое без доказательств за истинное.
вследущий раз в учебник смотри ВНИМАТЕЛЬНО
=16аб-3а^2-5б^2