Дано функцію f(x) = (x^2-8x)/(x+1)
Знаходимо найбільше і найменше значення даної функції на проміжку [-5,-2].
f(-5) = ((-5)^2-8*(-5))/(-5+1) = 65/(-4) = -16,25.
f(-2) = ((-2)^2-8*(-2))/(-2+1) = 20/(-1) = -20.
Визначаємо точки екстремуму даної функції.
Знаходимо первісну:
f'(x) = (2x-8)*(x+1) - 1*(x^2-8x))/((x+1)^2) = (x^2 + 2x - 8)/((x + 1)^2).
Прирівнюємо їі до 0 (достатьно чисельник):
x^2 + 2x - 8 = 0, Д = 4+4*8 = 36, х1 = (-2 - 6)/2 = -4, х2 = (-2 + 6)/2 = 2.
Знаходимо знаки первісної:
х = -5 -4 1 2 3
y' = 0,4375 0 -1,25 0 0,4375 .
У точці х = -4 маємо максимум функції,
f(-4) = ((-4)^2-8*(-4))/(-4+1) = 48/(-3) = -16.
Відповідь:
- найбільше значення даної функції на проміжку [-5,-2] дорівнює -16,
- найменше значення даної функції на проміжку [-5,-2] дорівнює -20,
- максимум функції у точці х = -4,
- мінімум функції у точці х = 2.
Пусть 1-й тракторист вспахивает поле за х час, тогда 2-й - за (х+2) час, тогда за один час 1-й тракторист вспашет 1/х часть поля, 2-й вспашет 1/(х+2) , а вместе за 1 час они вспашут 1/х+1/(х+2).
2час 55 мин = 2 ⁵⁵/₆₀ час = 2 ¹¹/₁₂ час
По условию:
1/х+1/(х+2)· 2 ¹¹/₁₂ = 1
1/х+1/(х+2)·³⁵/₁₂ = 1
1/х+1/(х+2)=¹²/₃₅
Переносим все в левую часть и сводим к общему знаменателю.
получим
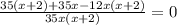
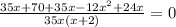
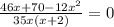
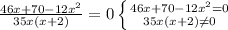
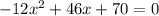
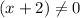
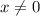
Решаем квадратное уравнение
6х²-23х-35=0
Д= 23²-4·6·9-35)=1369
√Д=37
х₁=(23+37)/12=5
х₂=(23-37)/12= - 14/12 - не удовлетворяет условию задачи.
1-й тракторист вспашет поле за 5 час, 2-й за 5+2=7 час
4240:100*20=848 книг
найдем количество справочников
848*3/4=636 книг
найдем количество учебников
4240-848-636=2756 книг