![E(y): y \in ( - \infty ; 4]](/tpl/images/1395/5414/90bc8.png)
Объяснение:
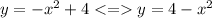
Графиком функции является парабола;
множитель при х² меньше нуля - ветви вниз.
Область определения: значение функции (у) может быть определено для любого значения аргумента (х)
D(y) = R
Точки экстремума (точки, в которых производная обращается в 0 или не определена:
y' = (-x^2+4)' \\ y'=-2x +0 =-2x
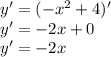
Найдем значение х для у'=0
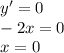
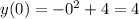
Для любого х > 0 у < 4
Для любого х < 0 у < 4
Точка (0;4) - точка максимума фунции.
Нижняя граница области значений функции отсутствует.
Следовательно, Область значений функции
E(y): y \in (- \inf ; 4]
![E(y): y \in (- \infty ; 4]](/tpl/images/1395/5414/abbe4.png)
1) x1=0 или 3х-4=0; х2=4/3=1целая1/3
ответ: 0 и 1 целая 1/3
2) х+4=0 или 2х-1=0
х=-4 х=0,5
ответ: -4 и 0,5