х км/ч собственная скорость катера
у км/ч скорость течения
По условию известно, что расстояние между двумя пунктами равно 14км, лодка проходит этот путь по течению за 2 ч, а против течения за 2 ч 48 мин= 2 48/60 = 2,8ч
Составим систему:
2(х+у) = 14 х+у = 7 х = 7-у
2,8(х-у) = 14 2,8(х-у)=14 2,8(7-у-у)=14
2,8(7-у-у)=14
7-2у = 5
2у = 2
у = 1
х = 7 - 1 = 6
ответ. 6 км/ч собственная скорость катера, 1 км/ч скорость течения.
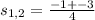
пусть х км/ч скорость катера, у км/ч- скорость теч.
2(х+у)=14
2.8(х-у)=14 система
из 1-го : 2х=14-2у
х=(14-2у) :2
х=7-у
подставляем во 2-ое
2.8(7-у-у)=14
19.6-5.6у=14
-5.6у=-5.6
у=1 км/ч скорость теч.
х=7-у=6 км/ч скорость лодки