Объяснение:5)5-2ax=14+2x; 6)3(8-3ах)=8-ах;
-2ax-2x=14-5; 24-9ах=8-ах;
-2x(a+1)=9; -9ах+ах=8-24;
x= - 9/2(a+1). 8ах=16
ур-ие имеет решение при ∀ а≠-1. ах=2 -
а≠0.
7)7х(а-8)=-5 -ур-ие имеет решение
при всех значениях а≠8.
8)3х(а+7)=7
ур-ие имеет решение при всех значениях а≠ -7.
1)
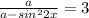
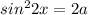
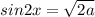
Так как значения синуса не могут быть большими единицы, получаем:
Так как выражение под радикалом и собственно весь радикал не могут быть отрицательными получаем:
Откуда получаем:
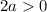
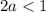
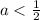
Объединяя полученные результаты получаем: a∈
ответ: a∈
2)
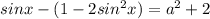
Получаем квадратное уравнение относительно t:
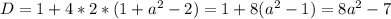
Исходя из того что данное уравнение должно иметь лишь одно решение получаем, что дискриминант должен быть равен нулю:
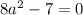
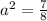
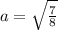
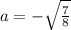
Но так как нам нужно только одно решение в заданном промежутке получаем:
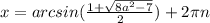
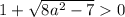
неравенство не имеет решений
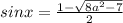
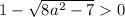
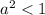
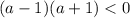
Получаем, что при a∈
данное уравнение имеет лишь один корень
ответ: a∈
Чтобы функция была нечётной, надо, чтобы выполнялось равенство:
f(-x) = - f(x)
То есть по сути дела: надо вместо х подставить -х, упростить( где можно) и сравнить с заданной функцией. ответы равные - функция чётная, ответы отличаются только знаком - нечётная; ни то, ни сё - функция ни чётная, ни нечётная.
а) f(x) = (x^4 + 4)/2x^3
f(-x) = ( (-x)^4 +4)/2(-x)^3 = (x^4 +4)/-2x^3= - (x^4 +4)/2x^3 = -f(x) ⇒
⇒f(x) - чётная
б) у = f(x) = (x^4 - Cos x)/(5x^3 - 3x)
f(-x) = ((-x)^4 - Cos(-x)) / (5(-x)^3 -3(-x)) = (x^4 - Cosx)/(-5x^3 +3x) =
= (x^4 - Cos x)/-(5x^3 - 3x)= - (x^4 - Cos x)/(5x^3 - 3x) = -f(x)⇒
⇒ f(x) - нечётная