Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
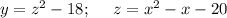
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
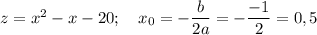 - координата вершины
- координата вершины
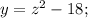 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
1.
p=34cm
a=x
b=x-3
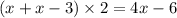
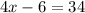

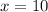
Длина 10, Ширина 10-3=7
2)
Известно, что туристическую группу из 38 человек расселили в двухместные и трёхместные номера.
При этом всего было занято 14 номеров.
Требуется вычислить сколько среди них было двухместных и сколько трёхместных.
Обозначим количество двухместных номеров "х", а количество трёхместных "у".
Тогда:
х + у = 14
х = 14 - у.
Составим уравнение.
2х + 3у = 38,
Подставим значение "х".
2 * (14 - у) + 3у = 38,
28 - 2у + 3у = 38,
у = 38 - 28 = 10 трёхместных номеров.
14 - 10 = 4 двухместных номеров.
15*100%/300=5% солі міститься в 300 грамах солі