Для того, чтобы найти значение cos a при tg a =2 и 0, воспользуемся следующей тригонометрической формулой: 1 + tg^2 a = 1 / (cos^2 a) и выразим из нее косинус.
1 + tg^2 a = 1 / (cos^2 a)
(1 + tg^2 a) * (cos^2 a) = 1
cos^2 a = 1 / (1 + tg^2 a)
cos a = sqrt (1 / (1 + tg^2 a)), где sqrt - корень квадратный.
Далее найдем косинус при значении tg a =2.
1) cos a = sqrt (1 / (1 + 2 ^2 )) = sqrt (1 / 5) = 0.4472
Далее найдем косинус при значении tg a = 0.
2) cos a = sqrt (1 / (1 + 0 ^2 )) = sqrt (1 / 1) = 1.
ответ: 0.4472, 1.
Объяснение:
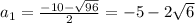
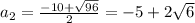
2х²+15х+25=2(х+5)(х-2,5)
-х²-4х+5=-(х+5)(х-1)
Подставляем lim (2(х+5)(х-2,5))/(-(х+5)(х-1))= сокращаем на х+5, вносим в первую скобку 2, а в знаменателе минус = lim(2х-5)/(1-х)=подставляем вместо х значение, к которому стремится -5 =(2*(-5)-5)/(1-(-5))=(-10-5)/6=-15/6=-2,5