1. нет; 2. 1) общего вида 2) общего вида 3) общего вида 3. 1) -1; 3 2) 1; -3 4) -1
Объяснение:
1. Если функция нечетная то произведение f(3)f(-3) не будет положительным.
2.
1)
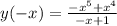
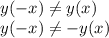
Это функция общего вида
2)
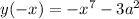
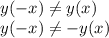
Это функция общего вида
3)
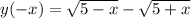
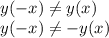
Это функция общего вида
3.
1)
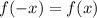
Значит
![min_{[2;4]}f(x)=min_{[-4;-2]}f(x)=-1\\max_{[2;4]}f(x)=max_{[-4;-2]}f(x)=3](/tpl/images/1407/6823/69e2d.png)
2)
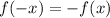
Значит
![min_{[2;4]}f(x)=-min_{[-4;-2]}f(x)=1\\max_{[2;4]}f(x)=-max_{[-4;-2]}f(x)=-3](/tpl/images/1407/6823/5cc0f.png)
4.
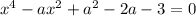
Это биквадратное уравнение. Делаем подстановку
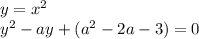
Уравнение будет иметь один корень, когда дискриминант равен 0
Но, поскольку х=±√у, то при любом положительном у мы получим два различных значения х. Одно значение х мы получим лишь в случае у=0. Тогда х=√0=0. Следовательно
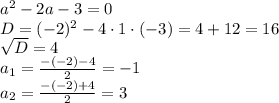
Делаем проверку:
1) а=-1

Имеется одно решение (т.к выражение в скобках никогда не будет равно 0)
2) а=3
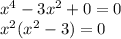
Здесь появляется второй корень. Значит, это значение не подходит.
Окончательно получаем решение: а=-1
На второй полке 32 книги, на третьей полке 40 книг.
Объяснение:
Будем считать, что в вопросе задачи опечатка, и требуется вместо яблок в корзинах найти количество книг на второй и третьей полках. Поэтому, так как по условию нам сказано, что на первой полке стоит 36 книг, а количество книг на второй полке составляет 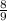 от количества книг на первой полке, поэтому приняв количество книг на первой полке за единицу а количество книг на второй полке за икс, составим пропорцию:
от количества книг на первой полке, поэтому приняв количество книг на первой полке за единицу а количество книг на второй полке за икс, составим пропорцию:
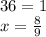
Откуда, принятое за x количество книг на второй полке будет равно:
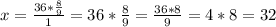 книги на второй полке.
книги на второй полке.
И эти 32 книги будут составлять 80% от количества книг на третьей полке, поэтому составляем еще одну пропорцию, приняв количество книг на третьей полке за 100%:
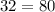 %
%
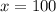 %
%
Аналогичным решения пропорции "крест на крест", находим количество книг на третьей полке:
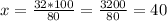 книг на третьей полке.
книг на третьей полке.
Получаем ответ: на второй полке 32 книги, на третьей полке 40 книг.
х₁-2,5=7
х₁=9,5
х₂-2,5=-7
х₂=-4,5
3-2х₁=0,2
х₁=-2,8:(-2)
х₁=1,4
3-2х₂=-0,2
х₂=-3,2:(-2)
х₂=1,6
6-х₁=11
х₁=-5
6-х₂=-11
х₂=17
5х₁+1=20
х₁=3,8
5х₂+1=-20
х₂=-4,2