11-(x+1)²≥x
11-x²-2x-1≥x
x²+3x-10≤0
x²+3x-10=0 D=49 √D=7
x₁=2 x₂=-5
(x-2)(x+5)≤0
-∞+-5___-2++∞ ⇒
ответ: x∈[-5;2]
(2x-8)²-4x*(2x-8)≥0
(2x-8)(2x-8-4x)≥0
(2x-8)(-2x-8)≥0
-(2x-8)*(2x+8)≥0 |÷(-1)
4x²-64≤0 |÷4
x²-16≤0
(x-4)(x+4)≤0
-∞+-4-4++∞ ⇒
ответ: x∈[-4;4].
x*(x+5)-2>4x
x²+5x-2-4x>0
x²+x-2>0
x²+x-2=0 D=9 √D=3
x₁=1 x₂=-2 ⇒
(x-1)(x+2)>0
-∞+-2-1++∞ ⇒
ответ: x∈(-∞-2)U(1;+∞).
(1/3)*x²+3x+6<0 |×3
x²+9x+18<0
x²+9x+18=0 D=9 √D=3
x₁=-3 x₂=-6 ⇒
(x+3)(x+6)<0
-∞+-6--3++∞ ⇒
ответ: x∈(-6;-3).
x>(x²/2)-4x+5¹/₂
x>(x²/2)-4x+11/2 |×2
2x>x²-8x+11
x²-10x+11<0
x²-10x+11=0 D=56 √D=√56
x₁=5-√14 x₂=5+√14
-∞+5-√14-5+√14++∞ ⇒
ответ: x∈(5-√14;5+√14).
, 
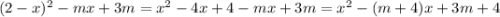
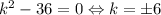
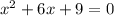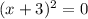, x = -3.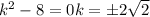
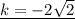
Решение:
При х≥3 |x-3| =х - 3
||x-3-3|-3|=3
||x-6|-3|=3
При х≥6 |x-6| =х - 6
|x-6-3|=3
|x-9|=3
При х≥9 |x-9| =х - 9
x-9 =3
x=12
Рассмотрим промежуточные интервалы
При 6≤х<9 |x-9| =9 - х
9 - x = 3
x = 9 - 3 = 6
При 3≤х<6 |x-6| = 6-x
|6-x-3|=3
|3-x|=3
так как мы приняли, что 3≤х<6 то |3-х| = x-3
х-3=3
х=6 ( не подходит так как 3≤х<6)
Следовательно для х≥3 уравнение имеет два корня 12 и 6.
При х<3 |x-3| = 3-x
||3-x-3|-3|=3
||-x|-3|=3
||x|-3|=3
при х<0 |x|=-x
|-x-3| =3
|x+3| =3
при х<-3 |x+3|=-x-3
-3-x=3
x=-6
Рассмотрим промежуточные интервалы
При -3≤х<0 |x+3| = х+3
x+3 = 3
x = 0 ( не подходит так как -3≤х<0)
При 0≤х<3 |x| = x
|x-3|=3
так как мы приняли, что 0≤х<3 то |х-3| = 3-х
3-х=3
х=0
Следовательно для х<3 уравнение имеет еще два корня -6 и 0.
ответ: -6;0;6;12