ответ:
объяснение:
в таблице простых чисел, то есть таких, которые делятся только на 1 и на себя, числа 7, 11 и 13 расположены рядом (см. таблицу простых чисел на стр. 363). их произведение равно:
7 ∙ 11 ∙ 13=1001 = 1000 + 1.
заметим пока, что 1000 + 1 делится и на 7, и на 11, и на 13. далее, если любое трехзначное число умножить на 1001, то произведение запишется такими же цифрами, как и множимое, только повторенными два раза.
пусть
— какое-либо трехзначное число (а, ь и с — цифры этого числа). умножим его на 1001:
следовательно, все числа вида аbсаbс делятся на 7, на 11 и на 13. в частности, делится на 7, 11 и 13 число 999 999, или, иначе, 1000 000—1.
указанные закономерности позволяют свести решение вопроса о делимости многозначного числа на 7 или на 11,
или на 13 к делимости на них некоторого другого числа — не более чем трехзначного.
требуется, положим, определить, делится ли число 42 623 295 на 7, 11 и 13. разобьем данное число справа налево на грани по 3 цифры. крайняя левая грань может и не иметь трех цифр. представим теперь данное число в гаком виде:
42 623 295 = 295 + 628 ∙ 1000 + 42 ∙ 1 000 000,
или (аналогично тому, как это мы делали при рассмотрении признака делимости на 11):
42 623 295 = 295 + 623 (1000 + 1 —1) + 42(1 — 1 + 1) = (295 — 623 + 42) + [623 (1000 + 1) + 42 (1000 000 —
число в квадратной скобке обязательно делится и на 7, и на 11, и на 13. значит, делимость испытуемого числа на
7, 11 и 13 полностью определяется делимостью числа, заключенного в первой круглой скобке.
рассматривая каждую грань испытуемого числа как самостоятельное число, можно высказать следующий объединенный признак делимости сразу на три числа, 7, 11 и 13:
вели разность сумм граней данного числа, взятых через одну, делится на 7 или на 11, или на 13, то и данное число делится соответственно на 7 или на 11, или на 13.
вернемся к числу 42 623 295. определим, на какое из чисел 7, 11 или 13 делится разность сумм граней данного числа:
(295 + 42)—623 = —286.
число 286 делится на 11 и на 13, а на 7 оно не делится. следовательно, число 42 623 295 делится на 11 и на 13, но на 7 не делится.
очевидно, что делимость на 7, 11 и 13 четырех-, пяти — и шестизначных чисел, то есть чисел, разбивающихся всего лишь на 2 грани (практически более частый случай), определяется делимостью на 7, 11 и 13 разности граней данного числа. так, например, легко установить, что 29 575 делится на 7 и на 13, но не делится на 11. действительно, разность граней равна
575—29 = 546,
а число 546 делится на 7 и на 13 и не делится на 11.
. устанавливая объединенный признак делимости на 7, 11 и 13, мы оперировали числом, разбивавшимся на 3 грани. проведите обоснование этого признака на примере числа, разбивающегося на 4 грани по 3 цифры справа налево.
S = 4
Объяснение:
Найдём уравнение прямой, проходящей через точки (-3; 0) и (-1; 3).
(х + 3)/(-1 + 3) = (у -0)/(3 - 0)
3(х + 3) = 2у
у = 1,5х + 4,5
Найдём точки пересечения этой прямой с осью Ох
у = 0;
1,5х + 4,5 = 0
х = -3
парабола у = 3х касается оси Ох в точке х = 0.
Найдём точки пересечения параболы у = 3х² и прямой у = 1,5х + 4,5
3х² = 1,5х + 4,5
3х² - 1,5х - 4,5 = 0
2х² - х - 3 = 0
D = 1 + 24 = 25
x1 = (1 - 5)/4 = -1
x2 = (1 + 5)/4 = 1.5
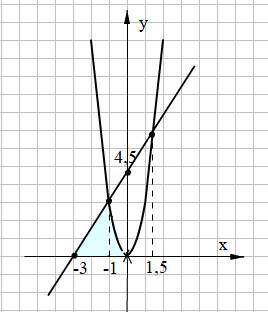
Изобразим графики, заданные уравнениями параболы и прямой.
Смотри рисунок на прикреплённом файле.
Очевидно, что фигура, заключённая между параболой, наклонной прямой и осью Ох, представляет собой криволинейный треугольник. Причем левая половина этого треугольника ограничена наклонной прямой и осью Ох, а правая половина - параболой и осью Ох. Соответственно, и интегралов будет два
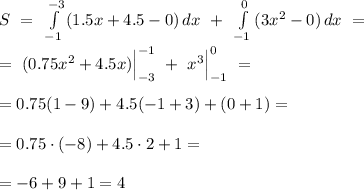
3y-8y=8-16+7
-5y=-1
y=5
-10+10x=2x-6+4
10x-2x=-6+4+10
8x=8
x=1