Здесь надо учесть четыре ограничения:
1) Подкоренное выражение не должно быть отрицательным:
![x^2-4^2\geqslant 0\\(x-4)(x+4) \geqslant 0\\x \in (- \infty; -4] \cup [4; + \infty)](/tpl/images/3214/7548/cb21f.png)
2) Выражение под логарифмом должно быть положительным: 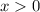
3) Знаменатель первой дроби должен быть ненулевым
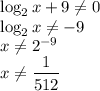
4) Знаменатель второй дроби также должен быть ненулевым:
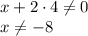
Теперь объединим эти промежутки (лучше сделайте это на листке бумаги, чтобы видеть наглядно): по второму условию икс положителен, поэтому первое условие сокращается до 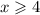
Третье условие не удовлетворяет предыдущему, поэтому вычёркивается.
Четвёртое условие также вычёркивается как отрицательное.
ответ: 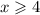
Вот так выглядит график этой функции, построенный на компьютере (см. скриншот).
P. S. Если появились какие-либо вопросы, задавайте.
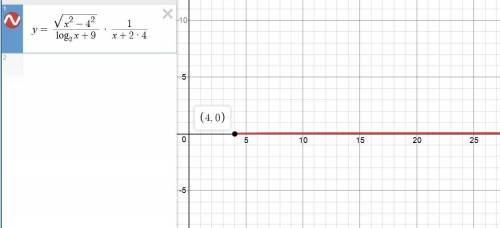
Объяснение:
Рассмотрим уравнение
t² - 4t + 5 = 0
D = 4² - 4*5 = 16 - 20 = -4
D = -4 < 0, следовательно уравнение не имеет действительных решений (график функции не пересекает ось Ох), график полностью находится в одной полуплоскости.
Рассмотрим значение коэффициента при старшей степени:
at² - bt + c
a = 1 > 0
Т.к. коэффициент при старшей степени положительный, ветви графика (парабола) направлена вверх.
График находится выше оси Ох, ветви направлены вверх, следовательно выражение t² - 4t + 5 при любом значении t принимает положительные значения
(X^9-x^3)+(x^8+x^7) +1
-2х^9 + 15х^56 +1