Водном доме на 88 квартир больше, чем в другом. сколько квартир в каждом доме, если в двух домах всего - id428055120220601 от Verra990 01.06.2022 08:12

Question

Алгебра: Водном доме на 88 квартир больше, чем в другом. сколько квартир в каждом доме, если в двух домах всего квартир 178.

Verra990 · Accepted Answer

При любом а, b и с график функции y=x^3 + ax^2 + bx+c имеет центр симметрии

Объяснение:

Решение в приложении

У кубической параболы будет всего один центр симметрии. В точке с абсциссой 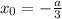$x_0=-\frac{a}{3}$ ординатой 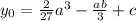$y_0=\frac{2}{27}a^3-\frac{ab}{3} +c$ . Эта точка совпадает с точкой перегиба.

Если посмотреть скриншоты, то только в случае 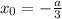$x_0=-\frac{a}{3}$ выполняется условие центра симметрии.

Это можно было бы доказать с параллельного переноса, растяжения и сжатия, поворота кубической параболы y=x³. Любая другая парабола получается из исходной с этих преобразований.

Интересно еще вот что, в формуле Кардано для решения кубического уравнения первая подстановка именно 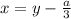$x=y-\frac{a}{3}$ .

При каких значениях а, b и с график функции y=x^3 + ax^2 + bx+c имеет центр симметрии?

Водном доме на 88 квартир больше, чем в другом. сколько квартир в каждом доме, если в двух домах всего квартир 178.

MOGZ ответил