Объяснение:
для начала строим первый график исходной функции
назовем его нулевым
(0) у=3*sin(x/2+pi/6)+1
простите великодушно, но этот график имеется в Вашем предыдущем задании, вы знаете как он выглядит, я лишь выложу готовый график во вложении. взгляните на него. (смотри во вложении).ок.
а) в этом графике зависимость от х совпадает с графиком (0) при положительных х, а при отрицательных график является зеркальным отображением себя относительно вертикальной оси У
(смотри во вложении)
б) этот график отличается от (0) тем, что те значения Y, которые были отрицательны вдруг стали положительны. получается что отрицательная часть графика перевернулась (отразилась) относительно оси Х
(смотри во вложении)
в) этот график отличается от графика а) тем что он как и предыдущий, развернул свои отрицательные значения вверх
(смотри во вложении)
г) строим график а) там где значения y были положительны.
модуль игрека говорит о том что у нас есть две ветки, симметричные относительно оси Х.
строим вторую ветку симметрично только что построенной относительно оси Х
замечание этот график неопределен в тех местах где график а) принимает отрицательные значения, там пропуски
д) этот график имеет две симметричные ветки относительно оси Х
построен может быть из (0) либо из(б) путем дорисовывания симметричной относительно оси Х части к имеющемуся графику
е)а этот график строится из графика в) путем добавления части симметричной исходному относительно оси Х
все графики есть во вложении
Чтобы найти область значения функции, надо сначала найти ординату вершины параболы(n), а для того чтобы найти ординату вершины параболы, надо сначала найти абсциссу вершины параболы по формуле m=-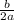
затем подставить вместо х значение m, а потом уже найти n:
m=- =-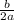
= -
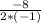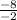= -4
< br/ > n = f(m) =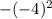
-8*(-4)+1 = -16+32+1=17
Мы нашли ординату вершины параболы. Это её наибольшее значение. Поэтому все остальные значения параболы будут либо меньше, либо равны 17(≤17).
Поэтому ответ таков: Е(у)=(-∞;17]. Если что, Е(у)- это область значения.
УДАЧИ ВАМ ВО ВСЁМ)))!
| x | = x при х ≥ 0
| x | = - x при х < 0 (*)
Найдём при каких х каждое выражение под модулем = 0
Это числа -3, 1 и 3. Числовая прямая этими числами разобьётся на промежутки. Сколько промежутков, столько и решений.Будем "снимать" знак модуля. учитывая (*)
-∞ -3 1 3 +∞
а) (-∞; -3)
- (х +3) -(х -1) -(х -3) < 10
-x - 3 - x +1 -x +3 <10
-3x < 9
x > -3 ( не входит в наш промежуток)
б) (-3;1)
х + 3 -(х - 1) -(х - 3) < 10
х + 3 - х +1 -х +3 < 10
- x < 3
x > -3
в) (1;3)
х + 3 + х - 1 -(х - 3) > 10
x + 3 + x - 1 - x + 3 > 10
x > 5 (не входит в наш промежуток)
г) (3;+∞)
х + 3 + х - 1 + х - 3 > 10
3x > 11
x > 11/3 ( входит в наш промежуток.
ответ: (-3;1) ∨ (11/3; +∞)