и 
. Чтобы найти координату 
точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
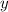можем найти подставив в выражение первой функции , а можно сделать проще. Так как пересечение будет с прямой , то и точки пересечения будут иметь координату . Итак, получилось две точки пересечения с координатами: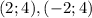 
.![[0;1]](/tpl/images/0561/5883/90495.png)
(этот отрезок по оси ), найдем значения 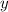на концах этого отрезка: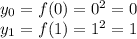
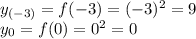
x(x+3)/(x-3)² : ( (3(x-3) +x²+9 +3(x+3)) /(x -3)(x+3) ) =
x(x+3)/(x-3)² : ( ( x²+6x +9) /(x -3)(x+3) ) =x(x+3)/(x-3)² : ( ( x+3)² /(x -3)(x+3) ) =
x(x+3)/(x-3)² * (x -3)/(x+3) =x/(x-3).
-----------------
A) ( (x+5y)/(x² -5y)-(x-5y)/(x² -5y) )* 5y²/(25y² -x²) =50y³/(x² -5y)(25y² -x²) .
-----------------
Б) ( (a -2b)/a(a+2b) -(a+2b)/a(a-2b) ) * (4b² -a²)/4b² =
(((a-2b)² -(a+2b)² ) /a(a² - 4b²))* (4b² -a²)/4b² =( 8b/(4b² -a²)) )* (4b² -a²)/4b² = 2 / b.
-----------------
г) =( C/(C-2) -C/(C+2) +(C²+4)/(C² - 4) ) *(C-2)²/C(C+2) =
( C² +2C -C² +2C +C² +4)/(C-2)(C+2) ) *(C-2)²/C(C+2) =
( (C +2)²/(C-2)(C+2) ) * (C-2)²/C(C+2) =(C-2) / C. || 1 -2/C ||