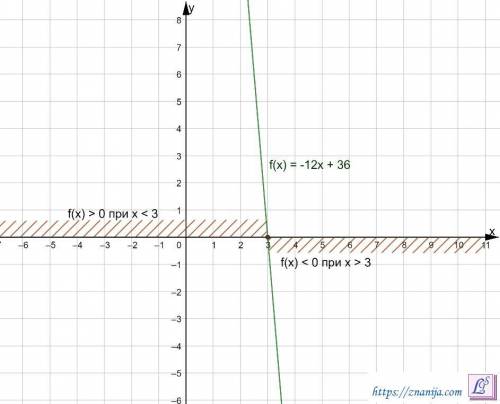
Функция f(x) = -12x + 36 убывающая.
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
f(x) = -12x + 36
Это линейная функция, ее график прямая линия. Общий вид линейной функции f(x) = kx + b.
Коэффициент k определяет угол наклона прямой к оси ОХ.
k = -12, k < 0, прямая проходит через II - IV четверти. (k < 0, угол между прямой и положительный направлением оси ОХ тупой)
⇒ Функция f(x) = -12x + 36 убывающая.
f(x) = 0; -12x + 36 = 0; 12x = 36; x = 3
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
Функция f(x) = -12x + 36 убывающая.
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
f(x) = -12x + 36
Это линейная функция, ее график прямая линия. Общий вид линейной функции f(x) = kx + b.
Коэффициент k определяет угол наклона прямой к оси ОХ.
k = -12, k < 0, прямая проходит через II - IV четверти. (k < 0, угол между прямой и положительный направлением оси ОХ тупой)
⇒ Функция f(x) = -12x + 36 убывающая.
f(x) = 0; -12x + 36 = 0; 12x = 36; x = 3
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
6х^2+3x - p = 0
D = 9 +4*6*p = 9 + 24p
x = [-3 +- (9 + 24p)^0.5]/12
x1 * x2^4 +x2 *x1^4=63/8