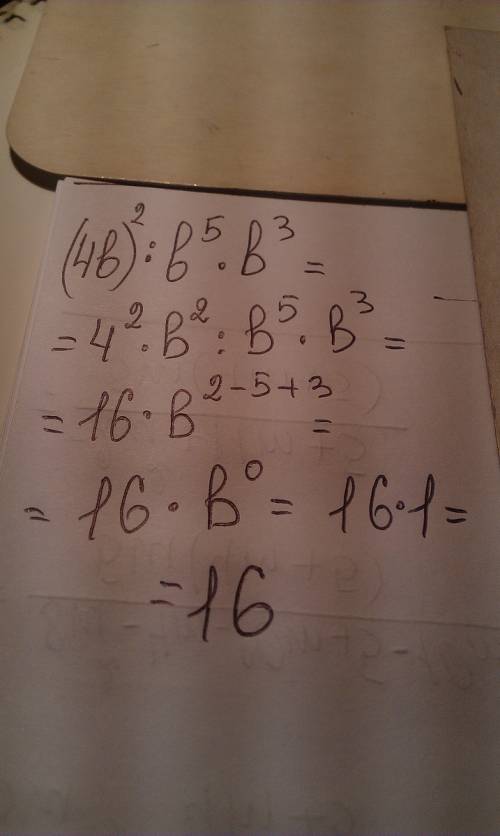
11457
Объяснение:
Требуется найти сумму чисел последовательности
aₓ=7·(x-1)+5, x=1, 2, ...
с ограничением aₓ<400.
Определим наибольший x:
aₓ<400 ⇔ 7·(x-1)+5<400 ⇔ 7·(x-1) < 395 ⇔ x-1 < 395/7 ⇔ x < 57 3/7.
Отсюда x=57 и тогда a₅₇=7·56+5=397.
Рассмотрим суммы чисел, составленные из 57 членов последовательности по возрастанию и по убыванию слагаемых:
S = 5 + 12 +...+ 390 + 397
S = 397+390+...+ 12 + 5
Сумма этих сумм равна
2·S=(5+397)+(12+397)+...+(390+12)+(397+5)=57·402=22914.
Делим на 2 и получим искомую сумму
S=11457.
Скорость лодки в неподвижной реке равна 15 км/ч.
Объяснение:
Пусть скорость лодки в неподвижной воде - х.
Для решения этой задачи нам требуется составить уравнение и решить его.
v(реки) = v(плота) = 3 км/ч. 48 км / 3 км/ч = 16 (ч) - плыл плот;
16 ч - 1 ч = 15 (ч) - плыла лодка (так как она отправилась через час, из условий).
Выходит уравнение:
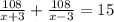Решаем его:
108(x - 3) + 108(x + 3) - 15(x - 3)(x + 3) = 0, где x ≠ 3 и х ≠ -3. <=>
108x - 324 + 108x + 324 - 15x² + 135 = 0
-15x² + 216x + 135 = 0
5x^2 - 72x - 45 = 0
D = 5184 + 900 = 6084. √D = √6084 = 78.
x₁ = (72 - 78) / 10 - не подходит по условию задачи
x₂ = (72 + 78) / 10 = 15 км/ч.
Мы за х взяли скорость в неподвижной реке, значит, х = 15 км/ч - это и есть ответ.
