а) x^2 + 4x + 10 >= 0
D = 4^2 - 4*10 = 16 - 40 = -24
a>0; D<0
(-∞;+∞)
ответ: 2. Решением неравенства является вся числовая прямая
b) - x^2 + 10x - 25 > 0/ *(-1)
x^2 - 10x + 25 < 0
D = -10^2 - 4 * 25 = 100 - 100 = 0
a>0; D=0
ответ: 1. Неравенство не имеет решений
с) x^2 + 3x + 2 <= 0
D = 3^2 - 4*2 = 9 - 8 = 1
a>0; D>0
x1 = -3 - 1/2 = -2
x2 = -3+1/2 = -1
[-2;-1]
ответ: 4. Решением неравенства является закрытый промежуток
d) -x^2 + 4 < 0/*(-1)
x^2 - 4 > 0
x^2 > 4/
x > 2
(2; +∞)
ответ: 5. Решением неравенства является открытый прпромежуток
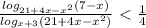
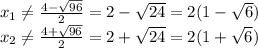
 ) U (
) U ( ; -2) U (-2;
; -2) U (-2;  ) U (
) U ( ; 7).
; 7).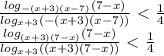
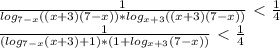
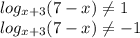
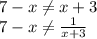
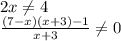
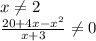
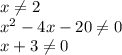
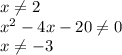
 ) U (
) U ( ; -2) U (-2; 2) U (2;
; -2) U (-2; 2) U (2;  ) U (
) U ( ; 7).
; 7).
ответ: отец будет старше сына в 5 раз через 4 года