2
Объяснение:
Рассмотрим наши три условия.
1) x - b < 0
Разность отрицательна, если уменьшаемое меньше вычитаемого.
⇒ x < b , значит число х расположено левее числа b на координатной прямой.
2) ax < 0
Число а расположено на координатной прямой левее 0. Значит оно отрицательно.
Произведение двух чисел отрицательно, если они имеют разные знаки.
⇒ число х положительно.
x > 0
3) c - b < x
Мы видим, что разница между с и b равна 1. Так как число с расположено правее числа b, то с > b и разность этих чисел положительна.
Действительно, числу b соответствует 3, числу с соответствует 4.
4 - 3 = 1
То есть x > 1.
Получили положительное число х, которое больше 1 и меньше 3.
1 < x < 3.
⇒ x = 2
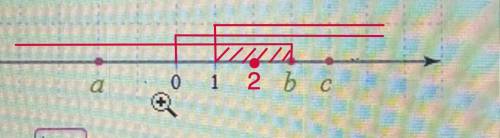
1. x² + 3x + 2 = x² + 2x + 1 + x + 1 = (x² + 2x + 1) + (x + 1) = (x + 1)² + (x + 1) = (x + 1)(x + 1 + 1) = (x + 1)(x + 2).
Можно разложить на множители и с теоремы:
ах² + bx + c = a(x - x1)(x - x2), где х1 и х2 - корни квадратного трёхчлена.
2. (с - а)(с + а) - b(b - 2a) = c² - a² - b² + 2ab = c² - (a² + b² - 2ab) = c² - (a - b)² =
применим формулу разности квадратов двух выражений, получим
= (c - (a-b))(c + (a-b)) = (с-а+b)(c+a-b).
3. a² - 3ab + 2b² = a² - 2ab + b² - ab + b² = (a² - 2ab + b²) - (ab - b²) = (a - b)² - b(a - b) = (a - b)(a - b - b) =
= (a - b)(a - 2b).
x^2 -y^2=3
x^2 -xy=2
Разложим оба уравнения системы на множители:
(х-у)*(х+у)=3
х*(х-у)=2
Разделим первое уравнение системы уравнений на второе уравнение:
(х-у)*(х+у)/х*(х-у)=3/2
(х+у)/х=3/2
2*(х+у)=3*х
2х+2у=3х
2х-3х=-2у
-х=-2у
х=-2у : -1
х=2у - подставим полученное значение (х) в первое уравнение системы уравнений:
(2у)^2 -y^2=3
4y^2-y^2=3
3y^2=3
y^2=3 : 3
y^2=1
у1,2=+-√1=+-1
у1=1
у2=-1
Подставим найденные значения (у) в х=2у:
х1=2*1
х1=2
х2=2*-1
х2=-2
ответ: х1=2; х2=-2; у1=1; у2=-1